1. Введение
Целью этой серии статей является объяснение идеи генетических алгоритмов и демонстрация наиболее известных реализаций .
В этом руководстве мы опишем концепцию оптимизации колонии муравьев (ACO), а затем приведем пример кода.
2. Как работает АСО
ACO — это генетический алгоритм, вдохновленный естественным поведением муравья. Чтобы полностью понять алгоритм ACO, нам необходимо ознакомиться с его основными понятиями:
- муравьи используют феромоны, чтобы найти кратчайший путь между домом и источником пищи
- феромоны быстро испаряются
- муравьи предпочитают использовать более короткие пути с более плотным феромоном
Давайте покажем простой пример ACO, используемый в задаче о коммивояжере . В следующем случае нам нужно найти кратчайший путь между всеми узлами в графе:
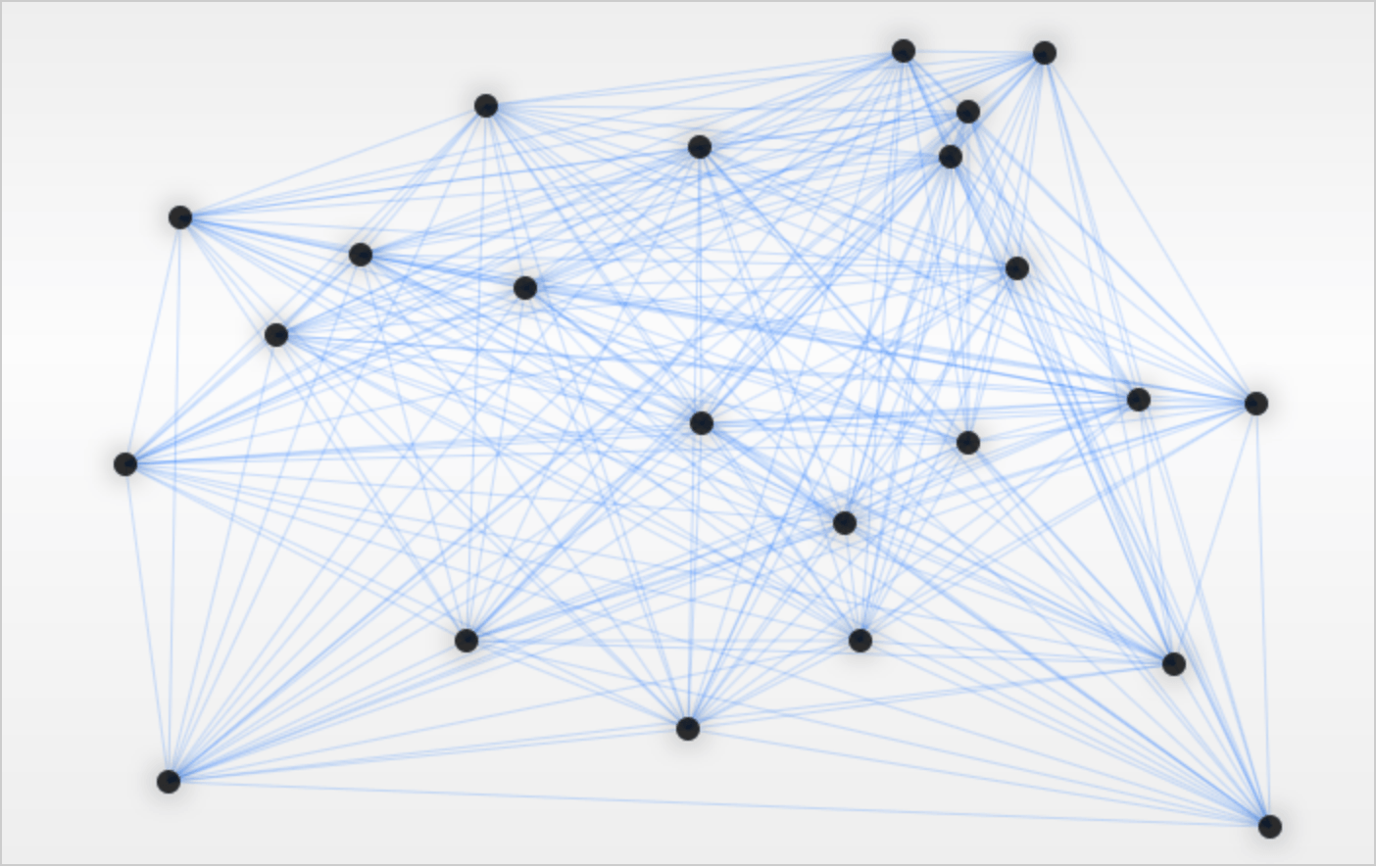
Следуя естественному поведению, муравьи начнут исследовать новые пути во время исследования. Более сильный синий цвет указывает на пути, которые используются чаще, чем другие, тогда как зеленый цвет указывает на текущий найденный кратчайший путь:
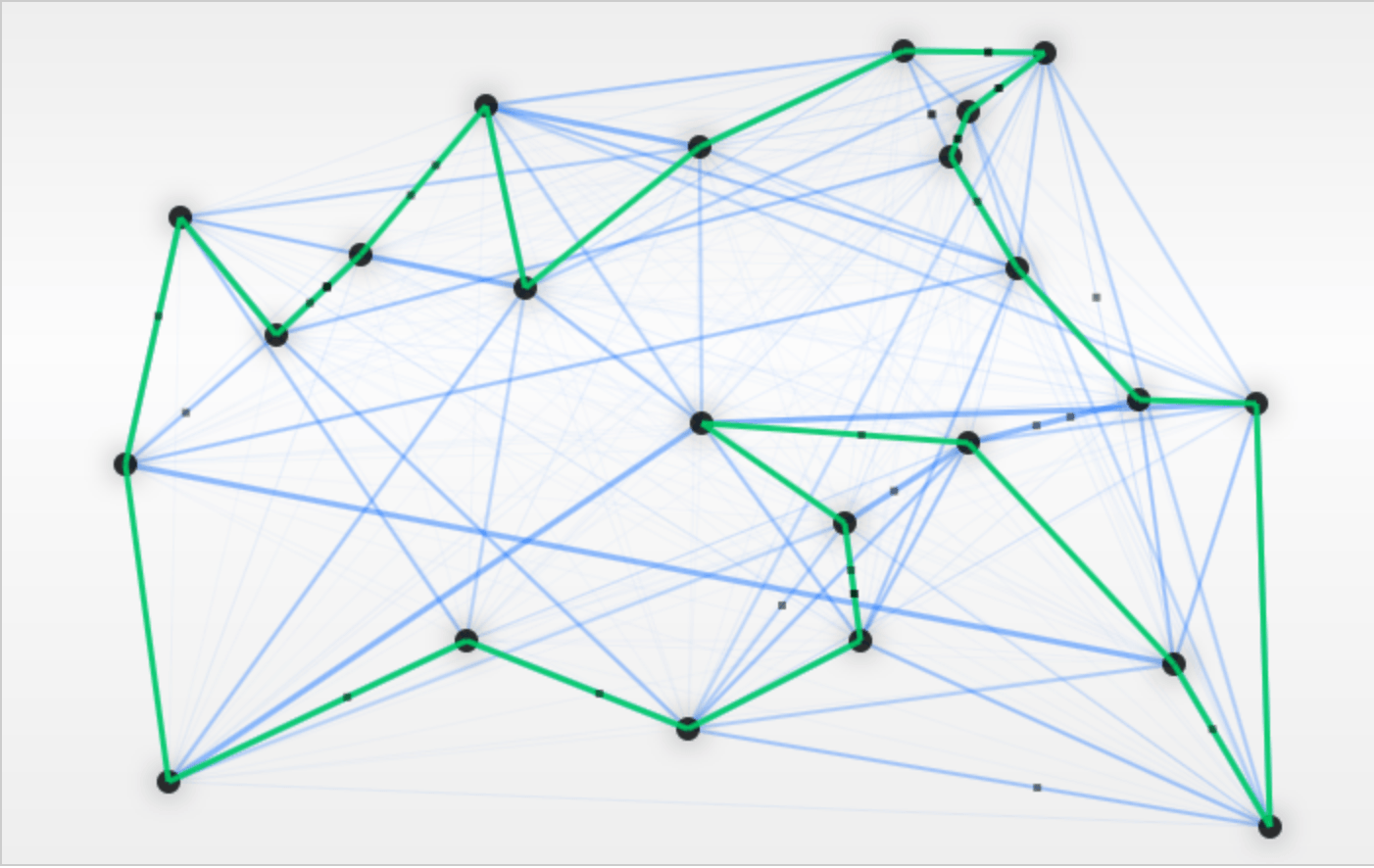
В результате мы получим кратчайший путь между всеми узлами:

Хороший инструмент для тестирования ACO с графическим интерфейсом можно найти здесь .
3. Реализация Java
3.1. Параметры АСО
Обсудим основные параметры алгоритма ACO, объявленные в классе AntColonyOptimization :
private double c = 1.0;
private double alpha = 1;
private double beta = 5;
private double evaporation = 0.5;
private double Q = 500;
private double antFactor = 0.8;
private double randomFactor = 0.01;
Параметр c указывает исходное количество следов в начале моделирования. Кроме того, альфа управляет важностью феромона, а бета управляет приоритетом расстояния. Как правило, для достижения наилучших результатов параметр бета должен быть больше, чем альфа .
Затем переменная evaporation показывает, сколько феромона испаряется в процентах за каждую итерацию, тогда как Q предоставляет информацию об общем количестве феромона, оставленного на следе каждым муравьем , а antFactor сообщает нам, сколько муравьев мы будем использовать в каждом городе.
Наконец, нам нужно немного случайности в наших симуляциях, и это покрывается randomFactor .
3.2. Создать муравьев
Каждый Муравей сможет посетить конкретный город, запомнить все посещенные города и отслеживать длину маршрута:
public void visitCity(int currentIndex, int city) {
trail[currentIndex + 1] = city;
visited[city] = true;
}
public boolean visited(int i) {
return visited[i];
}
public double trailLength(double graph[][]) {
double length = graph[trail[trailSize - 1]][trail[0]];
for (int i = 0; i < trailSize - 1; i++) {
length += graph[trail[i]][trail[i + 1]];
}
return length;
}
3.3. Настройка муравьев
В самом начале нам нужно инициализировать нашу реализацию кода ACO , предоставив матрицы следов и муравьев:
graph = generateRandomMatrix(noOfCities);
numberOfCities = graph.length;
numberOfAnts = (int) (numberOfCities * antFactor);
trails = new double[numberOfCities][numberOfCities];
probabilities = new double[numberOfCities];
ants = new Ant[numberOfAnts];
IntStream.range(0, numberOfAnts).forEach(i -> ants.add(new Ant(numberOfCities)));
Затем нам нужно настроить матрицу муравьев , чтобы начать со случайного города:
public void setupAnts() {
IntStream.range(0, numberOfAnts)
.forEach(i -> {
ants.forEach(ant -> {
ant.clear();
ant.visitCity(-1, random.nextInt(numberOfCities));
});
});
currentIndex = 0;
}
Для каждой итерации цикла мы будем выполнять следующие операции:
IntStream.range(0, maxIterations).forEach(i -> {
moveAnts();
updateTrails();
updateBest();
});
3.4. Переместить муравьев
Начнем с метода moveAnts() . Нам нужно выбрать следующий город для всех муравьев, помня, что каждый муравей старается идти по следам других муравьев:
public void moveAnts() {
IntStream.range(currentIndex, numberOfCities - 1).forEach(i -> {
ants.forEach(ant -> {
ant.visitCity(currentIndex, selectNextCity(ant));
});
currentIndex++;
});
}
Самая важная часть - правильно выбрать следующий город для посещения. Мы должны выбрать следующий город на основе вероятностной логики. Во- первых, мы можем проверить, должен ли Муравей посетить случайный город:
int t = random.nextInt(numberOfCities - currentIndex);
if (random.nextDouble() < randomFactor) {
OptionalInt cityIndex = IntStream.range(0, numberOfCities)
.filter(i -> i == t && !ant.visited(i))
.findFirst();
if (cityIndex.isPresent()) {
return cityIndex.getAsInt();
}
}
Если бы мы не выбрали ни одного случайного города, нам нужно рассчитать вероятности выбора следующего города, помня, что муравьи предпочитают следовать по более сильным и коротким тропам. Мы можем сделать это, сохранив вероятность переезда в каждый город в массиве:
public void calculateProbabilities(Ant ant) {
int i = ant.trail[currentIndex];
double pheromone = 0.0;
for (int l = 0; l < numberOfCities; l++) {
if (!ant.visited(l)){
pheromone
+= Math.pow(trails[i][l], alpha) * Math.pow(1.0 / graph[i][l], beta);
}
}
for (int j = 0; j < numberOfCities; j++) {
if (ant.visited(j)) {
probabilities[j] = 0.0;
} else {
double numerator
= Math.pow(trails[i][j], alpha) * Math.pow(1.0 / graph[i][j], beta);
probabilities[j] = numerator / pheromone;
}
}
}
После того, как мы вычислим вероятности, мы можем решить, в какой город идти, используя:
double r = random.nextDouble();
double total = 0;
for (int i = 0; i < numberOfCities; i++) {
total += probabilities[i];
if (total >= r) {
return i;
}
}
3.5. Обновить маршруты
На этом этапе мы должны обновить следы и левый феромон:
public void updateTrails() {
for (int i = 0; i < numberOfCities; i++) {
for (int j = 0; j < numberOfCities; j++) {
trails[i][j] *= evaporation;
}
}
for (Ant a : ants) {
double contribution = Q / a.trailLength(graph);
for (int i = 0; i < numberOfCities - 1; i++) {
trails[a.trail[i]][a.trail[i + 1]] += contribution;
}
trails[a.trail[numberOfCities - 1]][a.trail[0]] += contribution;
}
}
3.6. Обновите лучшее решение
Это последний шаг каждой итерации. Нам нужно обновить лучшее решение, чтобы сохранить ссылку на него:
private void updateBest() {
if (bestTourOrder == null) {
bestTourOrder = ants[0].trail;
bestTourLength = ants[0].trailLength(graph);
}
for (Ant a : ants) {
if (a.trailLength(graph) < bestTourLength) {
bestTourLength = a.trailLength(graph);
bestTourOrder = a.trail.clone();
}
}
}
После всех итераций окончательный результат укажет лучший путь, найденный ACO. Обратите внимание, что при увеличении количества городов уменьшается вероятность нахождения кратчайшего пути.
4. Вывод
В этом руководстве представлен алгоритм оптимизации муравьиной колонии . Вы можете узнать о генетических алгоритмах без каких-либо предварительных знаний в этой области, имея только базовые навыки компьютерного программирования.
Полный исходный код фрагментов кода в этом руководстве доступен в проекте GitHub .
Все статьи серии, включая другие примеры генетических алгоритмов, можно найти по следующим ссылкам:
- Как разработать генетический алгоритм на Java
- Задача коммивояжера в Java
- Оптимизация муравьиной колонии (это)