Перестановки массива в Java

1. Введение

В этой статье мы рассмотрим, как создавать перестановки массива .

Во-первых, мы определим, что такое перестановка. Во-вторых, мы рассмотрим некоторые ограничения. И в-третьих, мы рассмотрим три способа их вычисления: рекурсивный, итеративный и случайный.

Мы сосредоточимся на реализации на Java и поэтому не будем вдаваться в математические подробности.

2. Что такое перестановка?

Перестановка множества — это перестановка его элементов. Множество, состоящее из n элементов, имеет n! перестановки. Вот н! является факториалом, который является произведением всех положительных целых чисел, меньших или равных n .

2.1. Пример

Массив целых чисел [3,4,7] состоит из трех элементов и шести перестановок:

н! = 3! = 1 х 2 х 3 = 6

Перестановки: [3,4,7]; [3,7,4]; [4,7,3]; [4,3,7]; [7,3,4]; [7,4,3]

2.2. Ограничения

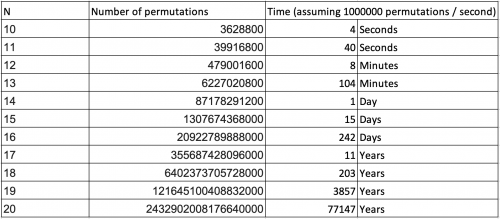
Число перестановок быстро увеличивается с n . Хотя для генерации всех перестановок из десяти элементов требуется всего несколько секунд, для генерации всех перестановок из 15 элементов потребуется две недели:

3. Алгоритмы

3.1. Рекурсивный алгоритм

Первый алгоритм, который мы рассмотрим, — это алгоритм Хипа . Это рекурсивный алгоритм, который производит все перестановки, заменяя один элемент за итерацию.

Входной массив будет изменен. Если мы этого не хотим, нам нужно создать копию массива перед вызовом метода:

public static <T> void printAllRecursive(
  int n, T[] elements, char delimiter) {

    if(n == 1) {
        printArray(elements, delimiter);
    } else {
        for(int i = 0; i < n-1; i++) {
            printAllRecursive(n - 1, elements, delimiter);
            if(n % 2 == 0) {
                swap(elements, i, n-1);
            } else {
                swap(elements, 0, n-1);
            }
        }
        printAllRecursive(n - 1, elements, delimiter);
    }
}

Метод использует два вспомогательных метода:

private void swap(T[] input, int a, int b) {
    T tmp = input[a];
    input[a] = input[b];
    input[b] = tmp;
}

private void printArray(T[] input) {
    System.out.print('\n');
    for(int i = 0; i < input.length; i++) {
        System.out.print(input[i]);
    }
}

Здесь мы записываем результат в System.out , однако вместо этого мы можем легко сохранить результат в массиве или в списке.

3.2. Итеративный алгоритм

Алгоритм кучи также можно реализовать с помощью итераций:

int[] indexes = new int[n];
int[] indexes = new int[n];
for (int i = 0; i < n; i++) {
    indexes[i] = 0;
}

printArray(elements, delimiter);

int i = 0;
while (i < n) {
    if (indexes[i] < i) {
        swap(elements, i % 2 == 0 ?  0: indexes[i], i);
        printArray(elements, delimiter);
        indexes[i]++;
        i = 0;
    }
    else {
        indexes[i] = 0;
        i++;
    }
}

3.3. Перестановки в лексикографическом порядке

Если элементы сопоставимы, мы можем генерировать перестановки, отсортированные по естественному порядку элементов:

public static <T extends Comparable<T>> void printAllOrdered(
  T[] elements, char delimiter) {

    Arrays.sort(elements);
    boolean hasNext = true;

    while(hasNext) {
        printArray(elements, delimiter);
        int k = 0, l = 0;
        hasNext = false;
        for (int i = elements.length - 1; i > 0; i--) {
            if (elements[i].compareTo(elements[i - 1]) > 0) {
                k = i - 1;
                hasNext = true;
                break;
            }
        }

        for (int i = elements.length - 1; i > k; i--) {
            if (elements[i].compareTo(elements[k]) > 0) {
                l = i;
                break;
            }
        }

        swap(elements, k, l);
        Collections.reverse(Arrays.asList(elements).subList(k + 1, elements.length));
    }
}

Этот алгоритм имеет обратную операцию на каждой итерации и поэтому менее эффективен для массивов, чем алгоритм Heap.

3.4. Рандомизированный алгоритм

Если n велико, мы можем сгенерировать случайную перестановку , перетасовав массив:

Collections.shuffle(Arrays.asList(elements));

Мы можем сделать это несколько раз, чтобы сгенерировать выборку перестановок.

Мы можем создавать одни и те же перестановки более одного раза, однако при больших значениях n вероятность создания одной и той же перестановки дважды невелика.

4. Вывод

Есть много способов сгенерировать все перестановки массива. В этой статье мы увидели рекурсивный и итеративный алгоритм кучи и то, как создать отсортированный список перестановок.

Невозможно сгенерировать все перестановки для больших массивов, поэтому вместо этого мы можем сгенерировать случайные перестановки.

Реализацию всех фрагментов кода в этой статье можно найти в нашем репозитории Github .