1. Введение
В этом руководстве мы познакомимся с деревом AVL и рассмотрим алгоритмы вставки, удаления и поиска значений.
2. Что такое дерево AVL?
Дерево AVL, названное в честь его изобретателей Адельсона-Вельского и Лэндиса, представляет собой самобалансирующееся двоичное дерево поиска (BST).
Самобалансирующееся дерево — это бинарное дерево поиска, которое уравновешивает высоту после вставки и удаления в соответствии с некоторыми правилами балансировки.
Временная сложность BST в наихудшем случае зависит от высоты дерева. В частности, самый длинный путь от корня дерева к узлу. Предположим, что для BST с N узлами у каждого узла есть только ноль или один дочерний элемент. Следовательно, его высота равна N, а время поиска в худшем случае равно O(N). Таким образом, наша главная цель в BST — сохранить максимальную высоту близкой к log(N).
Коэффициент баланса узла N равен height(right(N)) – height(left(N)) . В дереве AVL коэффициент баланса узла может принимать только одно из значений 1, 0 или -1.
Давайте определим объект Node для нашего дерева:
public class Node {
int key;
int height;
Node left;
Node right;
...
}
Далее давайте определим AVLTree :
public class AVLTree {
private Node root;
void updateHeight(Node n) {
n.height = 1 + Math.max(height(n.left), height(n.right));
}
int height(Node n) {
return n == null ? -1 : n.height;
}
int getBalance(Node n) {
return (n == null) ? 0 : height(n.right) - height(n.left);
}
...
}
3. Как сбалансировать дерево AVL?
Дерево AVL проверяет коэффициент баланса своих узлов после вставки или удаления узла. Если коэффициент баланса узла больше единицы или меньше -1, дерево перебалансируется.
Есть две операции по перебалансировке дерева:
- правое вращение и
- левое вращение.
3.1. Правое вращение
Начнем с правильного вращения.
Предположим, у нас есть BST с именем T1, с Y в качестве корневого узла, X в качестве левого потомка Y и Z в качестве правого потомка X. Учитывая характеристики BST, мы знаем, что X < Z < Y.
После правого поворота Y у нас есть дерево с именем T2 с X в качестве корня и Y в качестве правого дочернего элемента X и Z в качестве левого дочернего элемента Y. T2 все еще является BST, потому что он сохраняет порядок X < Z < Y .
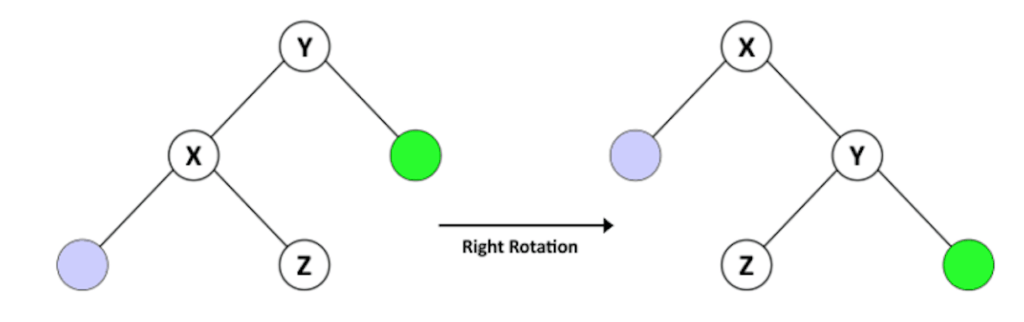
Давайте посмотрим на правильную операцию вращения для нашего AVLTree :
Node rotateRight(Node y) {
Node x = y.left;
Node z = x.right;
x.right = y;
y.left = z;
updateHeight(y);
updateHeight(x);
return x;
}
3.2. Операция левого вращения
У нас также есть операция левого вращения.
Предположим, что BST называется T1, с Y в качестве корневого узла, X в качестве правого потомка Y и Z в качестве левого потомка X. Учитывая это, мы знаем, что Y < Z < X.
После поворота Y влево у нас есть дерево с именем T2, где X является корнем, Y — левым дочерним элементом X, а Z — правым дочерним элементом Y. T2 по-прежнему является BST, поскольку сохраняет порядок Y < Z < X. .
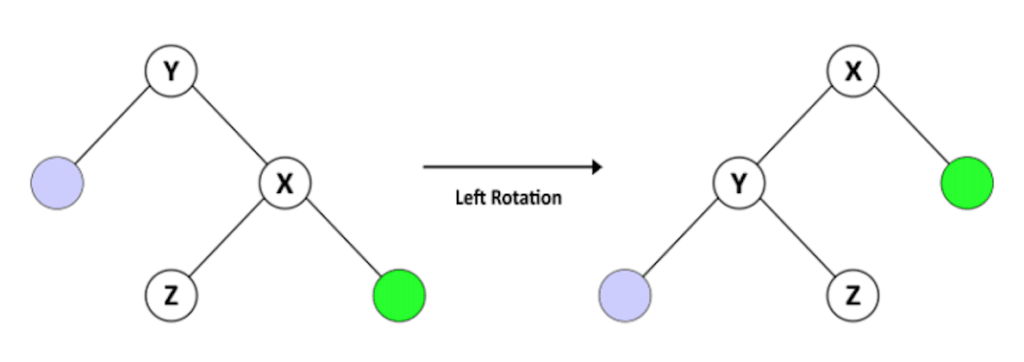
Давайте посмотрим на операцию поворота влево для нашего AVLTree :
Node rotateLeft(Node y) {
Node x = y.right;
Node z = x.left;
x.left = y;
y.right = z;
updateHeight(y);
updateHeight(x);
return x;
}
3.3. Методы ребалансировки
Мы можем использовать операции вращения вправо и влево в более сложных комбинациях, чтобы сохранить баланс дерева AVL после любых изменений в его узлах . В несбалансированной структуре хотя бы один узел имеет коэффициент баланса, равный 2 или -2. Давайте посмотрим, как мы можем сбалансировать дерево в этих ситуациях.
Когда коэффициент баланса узла Z равен 2, поддерево с Z в качестве корня находится в одном из этих двух состояний, считая Y правым дочерним элементом Z.
В первом случае высота правого потомка Y (X) больше высоты левого потомка (T2). Мы можем легко сбалансировать дерево, повернув Z влево.
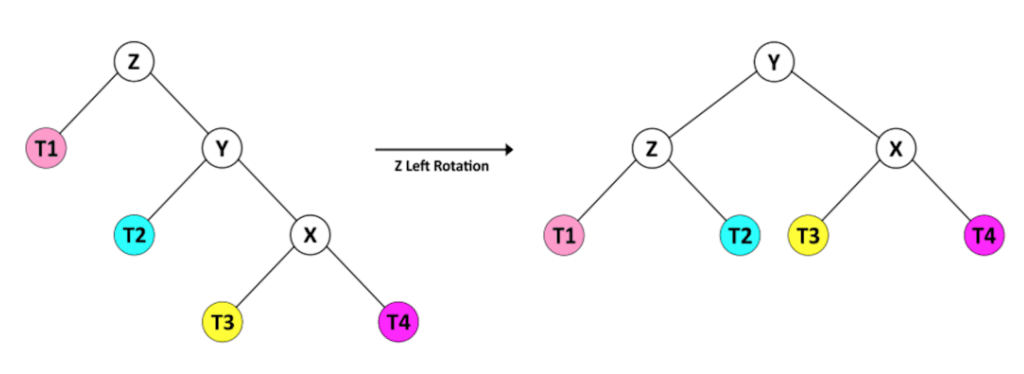
Во втором случае высота правого потомка Y (T4) меньше высоты левого потомка (X). В этой ситуации требуется комбинация операций вращения.
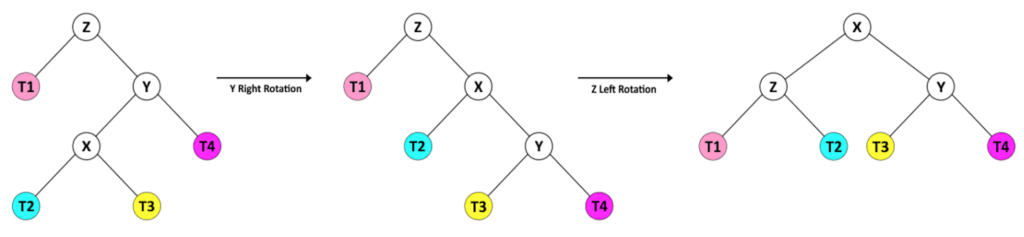
В этом случае мы сначала поворачиваем Y вправо, чтобы дерево приняло ту же форму, что и в предыдущем случае. Затем мы можем сбалансировать дерево, повернув Z влево.
Кроме того, когда коэффициент баланса узла Z равен -2, его поддерево находится в одном из этих двух состояний, поэтому мы рассматриваем Z как корень, а Y как его левый дочерний элемент.
Высота левого дочернего элемента Y больше высоты его правого дочернего элемента, поэтому мы уравновешиваем дерево правым вращением Z.
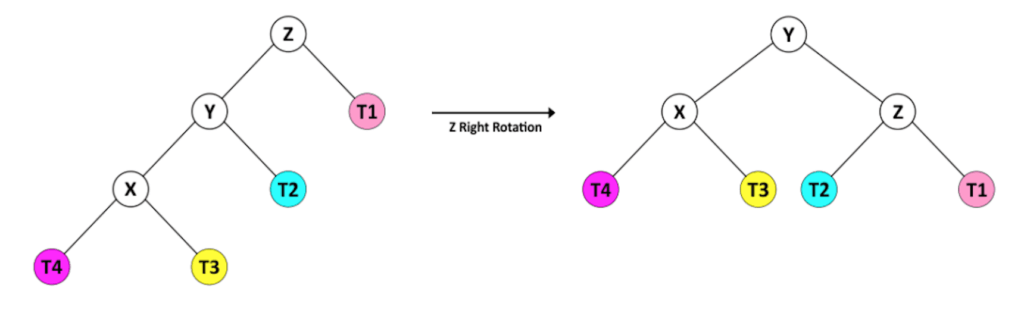
Или, во втором случае, правый потомок Y имеет большую высоту, чем его левый потомок.
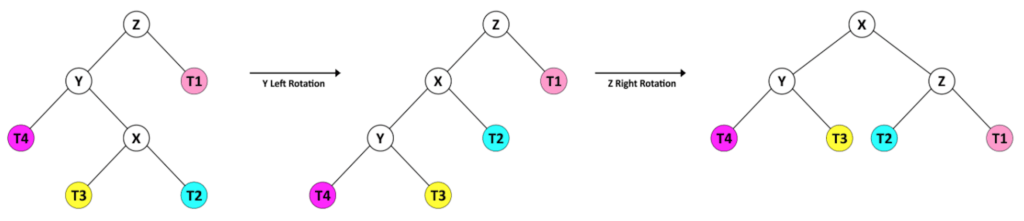
Итак, прежде всего, мы преобразуем его в прежнюю форму с левым вращением Y, затем балансируем дерево с правым вращением Z.
Давайте посмотрим на операцию перебалансировки для нашего AVLTree :
Node rebalance(Node z) {
updateHeight(z);
int balance = getBalance(z);
if (balance > 1) {
if (height(z.right.right) > height(z.right.left)) {
z = rotateLeft(z);
} else {
z.right = rotateRight(z.right);
z = rotateLeft(z);
}
} else if (balance < -1) {
if (height(z.left.left) > height(z.left.right))
z = rotateRight(z);
else {
z.left = rotateLeft(z.left);
z = rotateRight(z);
}
}
return z;
}
Мы будем использовать перебалансировку после вставки или удаления узла для всех узлов на пути от измененного узла к корню.
4. Вставьте узел
Когда мы собираемся вставить ключ в дерево, мы должны найти его правильное положение, чтобы пройти правила BST. Итак, мы начинаем с корня и сравниваем его значение с новым ключом. Если ключ больше, продолжаем вправо — иначе идем к левому потомку.
Как только мы находим правильный родительский узел, мы добавляем новый ключ в качестве узла слева или справа, в зависимости от значения.
После вставки узла у нас есть BST, но это может быть не дерево AVL. Поэтому мы проверяем факторы баланса и перебалансируем BST для всех узлов на пути от нового узла к корню.
Рассмотрим операцию вставки:
Node insert(Node node, int key) {
if (node == null) {
return new Node(key);
} else if (node.key > key) {
node.left = insert(node.left, key);
} else if (node.key < key) {
node.right = insert(node.right, key);
} else {
throw new RuntimeException("duplicate Key!");
}
return rebalance(node);
}
Важно помнить, что ключ уникален в дереве — никакие два узла не имеют одного и того же ключа.
Временная сложность алгоритма вставки зависит от высоты. Поскольку наше дерево сбалансировано, мы можем предположить, что временная сложность в худшем случае равна O(log(N)).
5. Удалить узел
Чтобы удалить ключ из дерева, мы сначала должны найти его в BST.
После того, как мы найдем узел (называемый Z), мы должны ввести нового кандидата, который станет его заменой в дереве. Если Z — лист, кандидат пуст. Если у Z есть только один ребенок, этот ребенок является кандидатом, но если у Z есть два ребенка, процесс немного сложнее.
Предположим, правый потомок Z называется Y. Сначала мы находим крайний левый узел Y и называем его X. Затем мы устанавливаем новое значение Z равным значению X и продолжаем удалять X из Y.
Наконец, мы вызываем метод перебалансировки в конце, чтобы сохранить BST в виде дерева AVL.
Вот наш метод удаления:
Node delete(Node node, int key) {
if (node == null) {
return node;
} else if (node.key > key) {
node.left = delete(node.left, key);
} else if (node.key < key) {
node.right = delete(node.right, key);
} else {
if (node.left == null || node.right == null) {
node = (node.left == null) ? node.right : node.left;
} else {
Node mostLeftChild = mostLeftChild(node.right);
node.key = mostLeftChild.key;
node.right = delete(node.right, node.key);
}
}
if (node != null) {
node = rebalance(node);
}
return node;
}
Временная сложность алгоритма удаления зависит от высоты дерева. Подобно методу вставки, мы можем предположить, что временная сложность в худшем случае равна O(log(N)).
6. Поиск узла
Поиск узла в дереве AVL такой же, как и в любом BST .
Начните с корня дерева и сравните ключ со значением узла. Если ключ равен значению, вернуть узел. Если ключ больше, ищите от правого дочернего элемента, в противном случае продолжайте поиск от левого дочернего элемента.
Временная сложность поиска зависит от высоты. Можно предположить, что временная сложность в худшем случае равна O(log(N)).
Давайте посмотрим пример кода:
Node find(int key) {
Node current = root;
while (current != null) {
if (current.key == key) {
break;
}
current = current.key < key ? current.right : current.left;
}
return current;
}
7. Заключение
В этом руководстве мы реализовали дерево AVL с операциями вставки, удаления и поиска.
Как всегда, вы можете найти код на Github .