1. Обзор
В этом уроке мы рассмотрим Java-реализацию алгоритма Борувки для нахождения минимального остовного дерева (MST) графа, взвешенного по ребрам .
Он предшествует алгоритмам Прима и Крускала , но все же может считаться чем-то средним между ними.
2. Алгоритм Борувки
Мы сразу перейдем к алгоритму. Давайте посмотрим немного на историю, а затем на сам алгоритм.
2.1. История
Способ нахождения MST данного графа был впервые сформулирован Отакаром Борувкой в 1926 году. Это было задолго до того, как появились компьютеры, и фактически он был смоделирован для разработки эффективной системы распределения электроэнергии.
Жорж Соллен заново открыл его в 1965 году и использовал в параллельных вычислениях.
2.2. Алгоритм
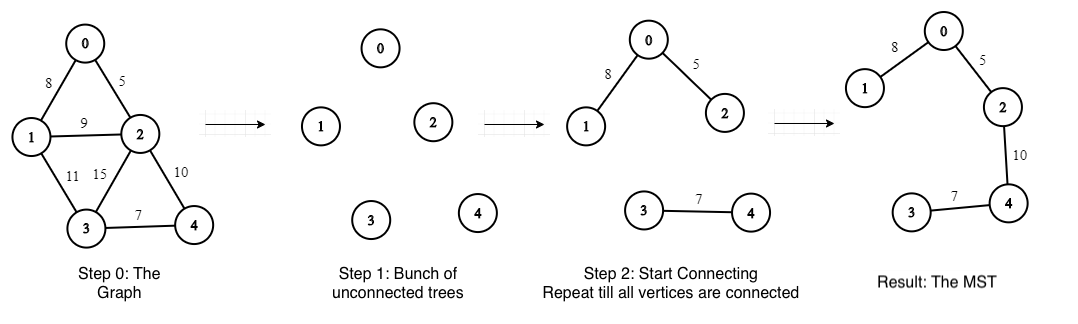
Основная идея алгоритма состоит в том, чтобы начать с набора деревьев, каждая вершина которого представляет собой изолированное дерево. Затем нам нужно продолжать добавлять ребра, чтобы уменьшить количество изолированных деревьев, пока у нас не получится одно связанное дерево.
Давайте рассмотрим это по шагам на примере графика:
Шаг 0: создайте график
Шаг 1: начните с набора несвязанных деревьев (количество деревьев = количеству вершин).
Шаг 2: пока есть несвязанные деревья, для каждого несвязанного дерева:
найти его ребро с меньшим весом
добавьте это ребро, чтобы соединить другое дерево
3. Реализация Java
Теперь давайте посмотрим, как мы можем реализовать это на Java.
3.1. Структура данных UnionFind
Для начала нам нужна структура данных для хранения родителей и рангов наших вершин .
Для этой цели определим класс UnionFind с двумя методами: union и find :
public class UnionFind {
private int[] parents;
private int[] ranks;
public UnionFind(int n) {
parents = new int[n];
ranks = new int[n];
for (int i = 0; i < n; i++) {
parents[i] = i;
ranks[i] = 0;
}
}
public int find(int u) {
while (u != parents[u]) {
u = parents[u];
}
return u;
}
public void union(int u, int v) {
int uParent = find(u);
int vParent = find(v);
if (uParent == vParent) {
return;
}
if (ranks[uParent] < ranks[vParent]) {
parents[uParent] = vParent;
} else if (ranks[uParent] > ranks[vParent]) {
parents[vParent] = uParent;
} else {
parents[vParent] = uParent;
ranks[uParent]++;
}
}
}
Мы можем думать об этом классе как о вспомогательной структуре для поддержания отношений между нашими вершинами и постепенного построения нашего MST.
Чтобы узнать, принадлежат ли две вершины u и v одному и тому же дереву, мы смотрим, возвращает ли find(u) того же родителя, что и find(v) . Метод объединения используется для объединения деревьев. Вскоре мы увидим это использование.
3.2. Введите график от пользователя
Теперь нам нужен способ получить вершины и ребра графа от пользователя и сопоставить их с объектами, которые мы можем использовать в нашем алгоритме во время выполнения.
Так как мы будем использовать JUnit для проверки нашего алгоритма, эта часть выполняется в методе @Before :
@Before
public void setup() {
graph = ValueGraphBuilder.undirected().build();
graph.putEdgeValue(0, 1, 8);
graph.putEdgeValue(0, 2, 5);
graph.putEdgeValue(1, 2, 9);
graph.putEdgeValue(1, 3, 11);
graph.putEdgeValue(2, 3, 15);
graph.putEdgeValue(2, 4, 10);
graph.putEdgeValue(3, 4, 7);
}
Здесь мы использовали MutableValueGraph<Integer, Integer> от Guava для хранения нашего графика. Затем мы использовали ValueGraphBuilder для построения неориентированного взвешенного графа.
Метод putEdgeValue принимает три аргумента: два Integer для вершин и третий Integer для веса, как указано в объявлении универсального типа MutableValueGraph .
Как мы видим, это тот же ввод, который показан на нашей диаграмме ранее.
3.3. Получите минимальное остовное дерево
Наконец, мы подошли к сути дела, реализации алгоритма.
Мы сделаем это в классе, который назовем BoruvkaMST . Во-первых, давайте объявим пару переменных экземпляра:
public class BoruvkaMST {
private static MutableValueGraph<Integer, Integer> mst = ValueGraphBuilder.undirected().build();
private static int totalWeight;
}
Как мы видим, здесь мы используем MutableValueGraph<Integer, Integer> для представления MST.
Во-вторых, мы определим конструктор, в котором происходит вся магия. Он принимает один аргумент — граф , который мы построили ранее.
Первое, что он делает, это инициализирует UnionFind вершин входного графа. Изначально все вершины являются своими родителями, ранг каждой равен 0:
public BoruvkaMST(MutableValueGraph<Integer, Integer> graph) {
int size = graph.nodes().size();
UnionFind uf = new UnionFind(size);
Далее мы создадим цикл, определяющий количество итераций, необходимых для создания MST — не более log V раз или до тех пор, пока у нас не будет ребер V-1, где V — количество вершин:
for (int t = 1; t < size && mst.edges().size() < size - 1; t = t + t) {
EndpointPair<Integer>[] closestEdgeArray = new EndpointPair[size];
Здесь мы также инициализируем массив ребер, ostestEdgeArray — для хранения ближайших ребер с меньшим весом.
После этого мы определим внутренний цикл for для перебора всех ребер графа, чтобы заполнить наш ближайшийEdgeArray .
Если родители двух вершин одинаковы, это одно и то же дерево, и мы не добавляем его в массив. В противном случае мы сравниваем вес текущего ребра с весом ребер его родительских вершин. Если меньше, то добавляем в ближайшийEdgeArray:
for (EndpointPair<Integer> edge : graph.edges()) {
int u = edge.nodeU();
int v = edge.nodeV();
int uParent = uf.find(u);
int vParent = uf.find(v);
if (uParent == vParent) {
continue;
}
int weight = graph.edgeValueOrDefault(u, v, 0);
if (closestEdgeArray[uParent] == null) {
closestEdgeArray[uParent] = edge;
}
if (closestEdgeArray[vParent] == null) {
closestEdgeArray[vParent] = edge;
}
int uParentWeight = graph.edgeValueOrDefault(closestEdgeArray[uParent].nodeU(),
closestEdgeArray[uParent].nodeV(), 0);
int vParentWeight = graph.edgeValueOrDefault(closestEdgeArray[vParent].nodeU(),
closestEdgeArray[vParent].nodeV(), 0);
if (weight < uParentWeight) {
closestEdgeArray[uParent] = edge;
}
if (weight < vParentWeight) {
closestEdgeArray[vParent] = edge;
}
}
Затем мы определим второй внутренний цикл для создания дерева. Мы добавим к этому дереву ребра из предыдущего шага, не добавляя одно и то же ребро дважды. Кроме того, мы выполним объединение нашего UnionFind , чтобы получить и сохранить родителей и ранги вершин вновь созданных деревьев:
for (int i = 0; i < size; i++) {
EndpointPair<Integer> edge = closestEdgeArray[i];
if (edge != null) {
int u = edge.nodeU();
int v = edge.nodeV();
int weight = graph.edgeValueOrDefault(u, v, 0);
if (uf.find(u) != uf.find(v)) {
mst.putEdgeValue(u, v, weight);
totalWeight += weight;
uf.union(u, v);
}
}
}
После повторения этих шагов не более log V раз или до тех пор, пока у нас не будет ребер V-1, результирующее дерево будет нашим MST.
4. Тестирование
Наконец, давайте посмотрим на простой JUnit для проверки нашей реализации:
@Test
public void givenInputGraph_whenBoruvkaPerformed_thenMinimumSpanningTree() {
BoruvkaMST boruvkaMST = new BoruvkaMST(graph);
MutableValueGraph<Integer, Integer> mst = boruvkaMST.getMST();
assertEquals(30, boruvkaMST.getTotalWeight());
assertEquals(4, mst.getEdgeCount());
}
Как мы видим, мы получили MST с весом 30 и 4 ребра, как и в наглядном примере .
5. Вывод
В этом уроке мы увидели реализацию алгоритма Борувки на Java. Его временная сложность равна O(E log V), где E — количество ребер, а V — количество вершин .
Как всегда, исходный код доступен на GitHub .