1. Введение
В этом уроке мы узнаем об алгоритме градиентного спуска . Мы реализуем алгоритм на Java и проиллюстрируем его шаг за шагом.
2. Что такое градиентный спуск?
Градиентный спуск — это алгоритм оптимизации, используемый для поиска локального минимума заданной функции. Он широко используется в высокоуровневых алгоритмах машинного обучения для минимизации функций потерь.
Градиент — это еще одно слово для обозначения уклона, а спуск означает спуск. Как следует из названия, градиентный спуск идет вниз по склону функции, пока не достигнет конца.
3. Свойства градиентного спуска
Градиентный спуск находит локальный минимум, который может отличаться от глобального минимума. Начальная локальная точка задается в качестве параметра алгоритма.
Это итеративный алгоритм , и на каждом этапе он пытается двигаться вниз по склону и приближаться к локальному минимуму.
На практике алгоритм работает с возвратом . В этом уроке мы проиллюстрируем и реализуем градиентный спуск с возвратом.
4. Пошаговая иллюстрация
Градиентному спуску нужна функция и отправная точка в качестве входных данных. Давайте определим и начертим функцию:
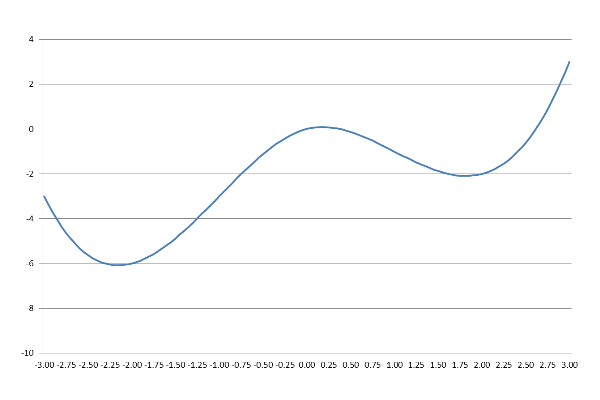
Мы можем начать в любой желаемой точке. Начнем с х = 1:
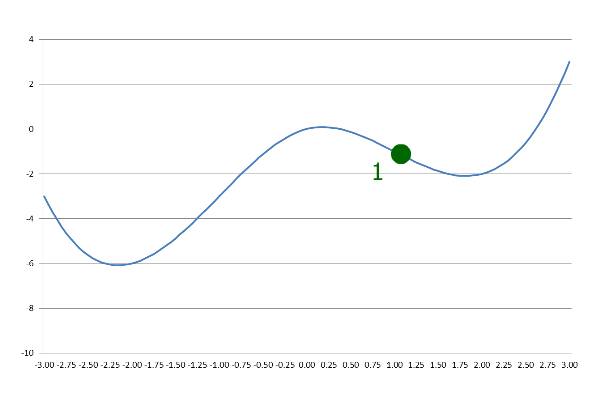
На первом этапе Gradient Descent спускается по склону с заранее заданным размером шага:
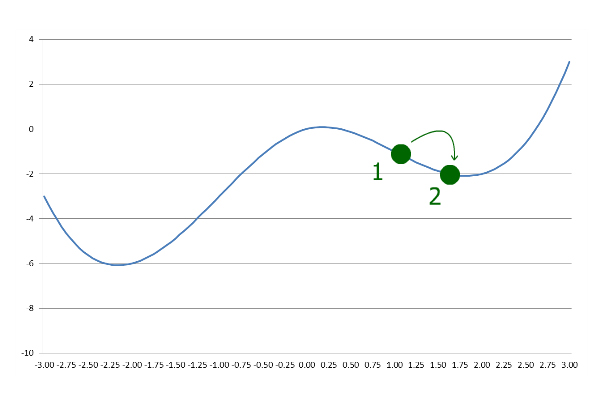
Далее он идет дальше с тем же размером шага. Однако на этот раз он заканчивается на большем y , чем на последнем шаге:
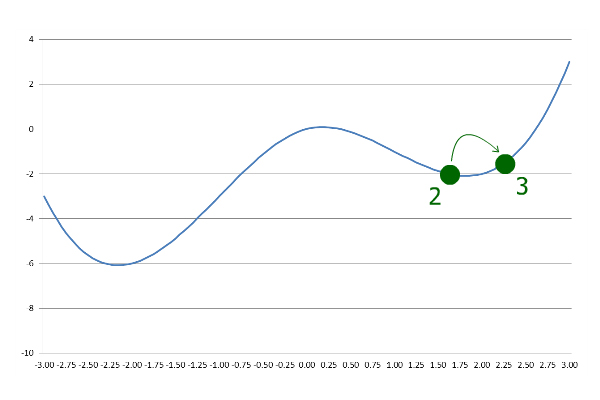
Это указывает на то, что алгоритм прошел локальный минимум, поэтому он возвращается с уменьшенным размером шага:
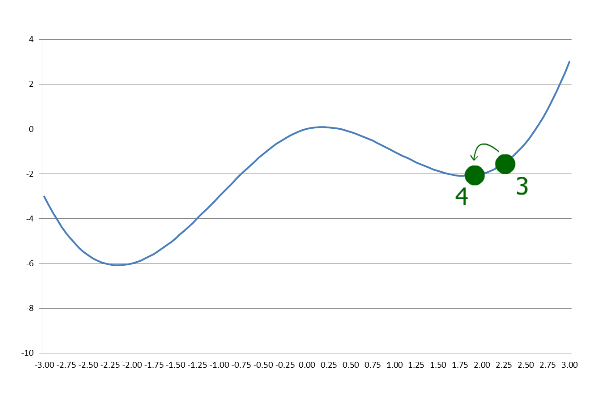
Впоследствии, всякий раз, когда текущий y больше, чем предыдущий y , размер шага уменьшается и инвертируется. Итерация продолжается до тех пор, пока не будет достигнута желаемая точность.
Как мы видим, Gradient Descent нашел здесь локальный минимум, но это не глобальный минимум. Если мы начнем с x = -1 вместо x = 1, будет найден глобальный минимум.
5. Реализация на Java
Существует несколько способов реализации градиентного спуска. Здесь мы не вычисляем производную функции, чтобы найти направление наклона, поэтому наша реализация работает и для недифференцируемых функций.
Давайте определим точность и stepCoefficient и присвоим им начальные значения:
double precision = 0.000001;
double stepCoefficient = 0.1;
На первом этапе у нас нет предыдущего y для сравнения. Мы можем либо увеличить, либо уменьшить значение x , чтобы увидеть, снижается или повышается y . Положительный stepCoefficient означает, что мы увеличиваем значение x .
Теперь давайте выполним первый шаг:
double previousX = initialX;
double previousY = f.apply(previousX);
currentX += stepCoefficient * previousY;
В приведенном выше коде f — это Function<Double, Double> , а initialX — это double , оба значения предоставляются в качестве входных данных.
Еще один ключевой момент, который следует учитывать, заключается в том, что сходимость градиентного спуска не гарантируется. Чтобы не застрять в цикле, давайте ограничим количество итераций:
int iter = 100;
Позже мы будем уменьшать iter на единицу на каждой итерации. Следовательно, мы выйдем из цикла максимум через 100 итераций.
Теперь, когда у нас есть предыдущийX , мы можем настроить наш цикл:
while (previousStep > precision && iter > 0) {
iter--;
double currentY = f.apply(currentX);
if (currentY > previousY) {
stepCoefficient = -stepCoefficient/2;
}
previousX = currentX;
currentX += stepCoefficient * previousY;
previousY = currentY;
previousStep = StrictMath.abs(currentX - previousX);
}
На каждой итерации мы вычисляем новый y и сравниваем его с предыдущим y . Если currentY больше, чем previousY , мы меняем наше направление и уменьшаем размер шага.
Цикл продолжается до тех пор, пока размер нашего шага не станет меньше желаемой точности . Наконец, мы можем вернуть currentX как локальный минимум:
return currentX;
6. Заключение
В этой статье мы рассмотрели алгоритм градиентного спуска с пошаговой иллюстрацией.
Мы также реализовали Gradient Descent на Java. Код доступен на GitHub .