1. Введение
В этом руководстве мы познакомим вас с жадными алгоритмами в экосистеме Java.
2. Жадная проблема
Столкнувшись с математической задачей, может быть несколько способов разработать решение. Мы можем реализовать итеративное решение или некоторые передовые методы, такие как принцип «разделяй и властвуй» (например , алгоритм быстрой сортировки ) или подход с динамическим программированием (например , задача о рюкзаке ) и многое другое.
Большую часть времени мы ищем оптимальное решение, но, к сожалению, не всегда получаем такой результат. Однако бывают случаи, когда ценен даже неоптимальный результат. С помощью некоторых конкретных стратегий или эвристик мы могли бы заработать себе такую драгоценную награду.
В этом контексте для делимой задачи стратегия, которая на каждом этапе процесса делает локально оптимальный выбор или «жадный выбор» , называется жадным алгоритмом.
Мы заявили, что должны решать «делимую» проблему: ситуацию, которую можно описать как набор подзадач с почти одинаковыми характеристиками. Как следствие, большую часть времени жадный алгоритм будет реализован как рекурсивный алгоритм .
Жадный алгоритм может привести нас к разумному решению, несмотря на суровые условия; отсутствие вычислительных ресурсов, ограничение времени выполнения, ограничения API или любые другие ограничения.
2.1. Сценарий
В этом коротком руководстве мы собираемся реализовать жадную стратегию для извлечения данных из социальной сети с использованием ее API.
Допустим, мы хотим охватить больше пользователей в социальной сети «маленькая синяя птичка». Лучший способ достичь нашей цели — опубликовать оригинальный контент или ретвитнуть что-то, что вызовет интерес у широкой аудитории.
Как найти такую аудиторию? Что ж, мы должны найти учетную запись с большим количеством подписчиков и твитнуть для них какой-нибудь контент.
2.2. Классический против жадного
Учитываем следующую ситуацию: На нашем аккаунте четыре подписчика, у каждого из которых, как изображено на изображении ниже, соответственно 2, 2, 1 и 3 подписчика и так далее:
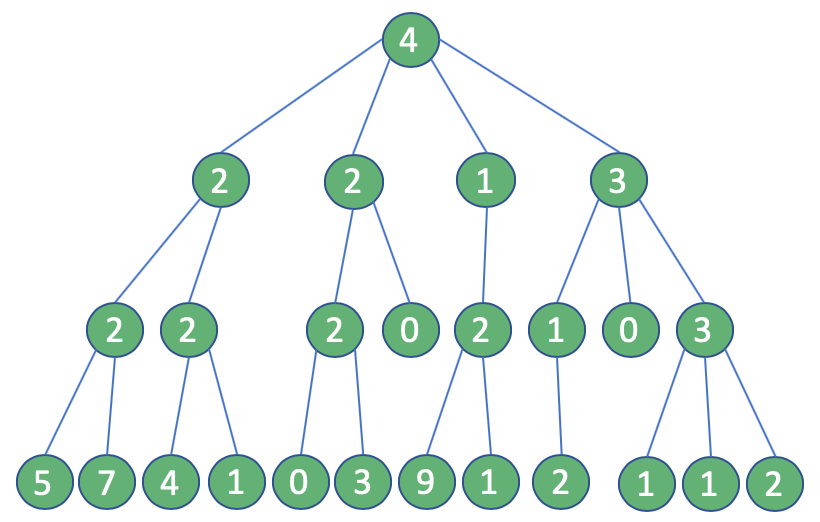
С этой целью мы возьмем того, у кого больше подписчиков среди подписчиков нашего аккаунта. Затем мы повторим процесс еще два раза, пока не достигнем 3-й степени связи (всего четыре шага).
Таким образом, мы определяем путь, состоящий из пользователей, который ведет нас к самой обширной базе подписчиков из нашей учетной записи. Если мы сможем адресовать им какой-то контент, они обязательно попадут на нашу страницу.
Мы можем начать с «традиционного» подхода. На каждом этапе мы будем выполнять запрос, чтобы получить подписчиков учетной записи. В результате нашего процесса отбора количество учетных записей будет увеличиваться с каждым шагом.
Удивительно, но в итоге мы выполнили 25 запросов:
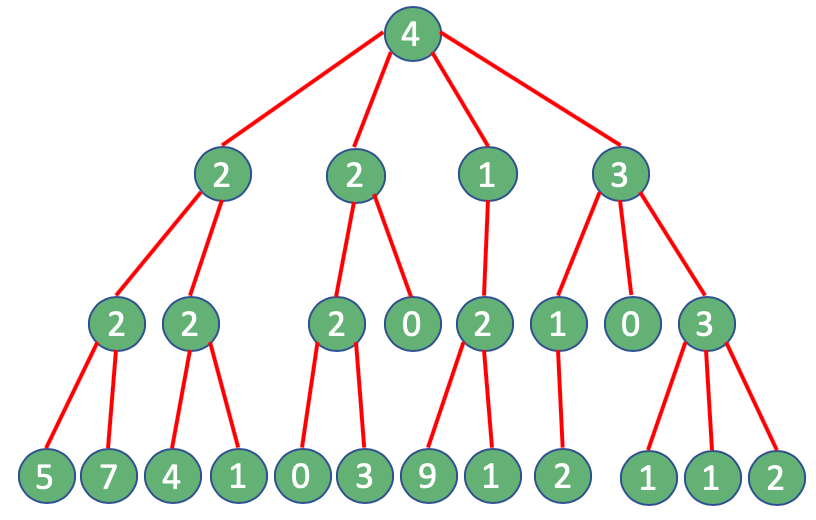
Здесь возникает проблема: например, Twitter API ограничивает этот тип запросов до 15 каждые 15 минут. Если мы попытаемся выполнить больше вызовов, чем разрешено, мы получим « Код превышения ограничения скорости — 88 » или « Возвращено в API версии 1.1, когда запрос не может быть обслужен из-за исчерпания предела скорости приложения для ресурса. “. Как мы можем преодолеть такой предел?
Что ж, ответ прямо перед нами: жадный алгоритм. Если мы используем этот подход, на каждом этапе мы можем предположить, что пользователь с наибольшим количеством подписчиков является единственным, кого следует учитывать: в конце концов нам нужно всего четыре запроса. Несомненное улучшение!
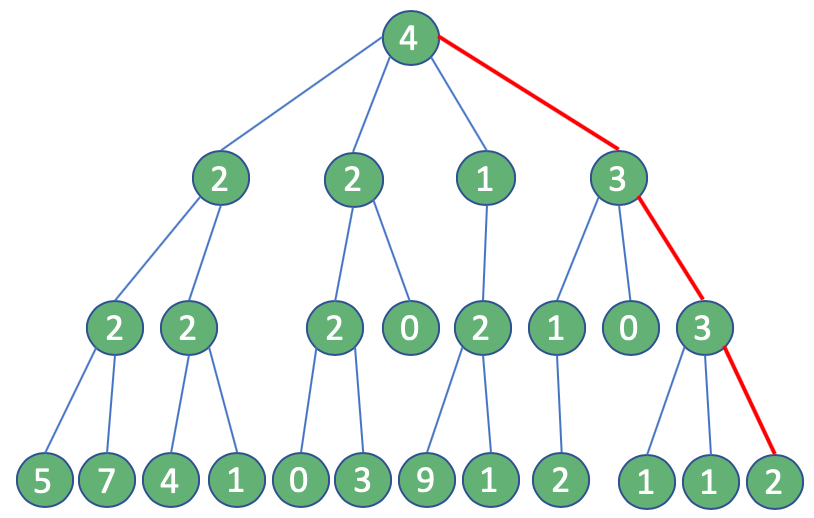
Результат этих двух подходов будет разным. В первом случае мы получаем 16, оптимальное решение, а во втором максимальное количество достижимых последователей составляет всего 12.
Будет ли эта разница столь ценна? Мы решим позже.
3. Реализация
Чтобы реализовать описанную выше логику, мы инициализируем небольшую программу на Java, в которой будем имитировать API Twitter. Мы также будем использовать библиотеку Lombok .
Теперь давайте определим наш компонент SocialConnector, в котором мы будем реализовывать нашу логику. Обратите внимание, что мы собираемся поставить счетчик для имитации ограничения вызовов, но мы уменьшим его до четырех:
public class SocialConnector {
private boolean isCounterEnabled = true;
private int counter = 4;
@Getter @Setter
List users;
public SocialConnector() {
users = new ArrayList<>();
}
public boolean switchCounter() {
this.isCounterEnabled = !this.isCounterEnabled;
return this.isCounterEnabled;
}
}
Затем мы добавим метод для получения списка подписчиков определенной учетной записи:
public List getFollowers(String account) {
if (counter < 0) {
throw new IllegalStateException ("API limit reached");
} else {
if (this.isCounterEnabled) {
counter--;
}
for (SocialUser user : users) {
if (user.getUsername().equals(account)) {
return user.getFollowers();
}
}
}
return new ArrayList<>();
}
Для поддержки нашего процесса нам нужны некоторые классы для моделирования нашей пользовательской сущности:
public class SocialUser {
@Getter
private String username;
@Getter
private List<SocialUser> followers;
@Override
public boolean equals(Object obj) {
return ((SocialUser) obj).getUsername().equals(username);
}
public SocialUser(String username) {
this.username = username;
this.followers = new ArrayList<>();
}
public SocialUser(String username, List<SocialUser> followers) {
this.username = username;
this.followers = followers;
}
public void addFollowers(List<SocialUser> followers) {
this.followers.addAll(followers);
}
}
3.1. Жадный алгоритм
Наконец, пришло время реализовать нашу жадную стратегию, поэтому давайте добавим новый компонент — GreedyAlgorithm — в котором мы будем выполнять рекурсию:
public class GreedyAlgorithm {
int currentLevel = 0;
final int maxLevel = 3;
SocialConnector sc;
public GreedyAlgorithm(SocialConnector sc) {
this.sc = sc;
}
}
Затем нам нужно вставить метод findMostFollowersPath, в котором мы найдем пользователя с наибольшим количеством подписчиков, посчитаем их, а затем перейдем к следующему шагу:
public long findMostFollowersPath(String account) {
long max = 0;
SocialUser toFollow = null;
List followers = sc.getFollowers(account);
for (SocialUser el : followers) {
long followersCount = el.getFollowersCount();
if (followersCount > max) {
toFollow = el;
max = followersCount;
}
}
if (currentLevel < maxLevel - 1) {
currentLevel++;
max += findMostFollowersPath(toFollow.getUsername());
}
return max;
}
Помните: здесь мы совершаем жадный выбор. Таким образом, каждый раз, когда мы вызываем этот метод, мы выбираем один и только один элемент из списка и идем дальше: мы никогда не откажемся от своих решений!
Идеальный! Мы готовы к работе и можем протестировать наше приложение. Перед этим нам нужно не забыть заполнить нашу крошечную сеть и, наконец, выполнить следующий модульный тест:
public void greedyAlgorithmTest() {
GreedyAlgorithm ga = new GreedyAlgorithm(prepareNetwork());
assertEquals(ga.findMostFollowersPath("root"), 5);
}
3.2. Нежадный алгоритм
Давайте создадим нежадный метод, просто чтобы проверить своими глазами, что происходит. Итак, нам нужно начать с создания класса NonGreedyAlgorithm :
public class NonGreedyAlgorithm {
int currentLevel = 0;
final int maxLevel = 3;
SocialConnector tc;
public NonGreedyAlgorithm(SocialConnector tc, int level) {
this.tc = tc;
this.currentLevel = level;
}
}
Давайте создадим эквивалентный метод для получения подписчиков:
public long findMostFollowersPath(String account) {
List<SocialUser> followers = tc.getFollowers(account);
long total = currentLevel > 0 ? followers.size() : 0;
if (currentLevel < maxLevel ) {
currentLevel++;
long[] count = new long[followers.size()];
int i = 0;
for (SocialUser el : followers) {
NonGreedyAlgorithm sub = new NonGreedyAlgorithm(tc, currentLevel);
count[i] = sub.findMostFollowersPath(el.getUsername());
i++;
}
long max = 0;
for (; i > 0; i--) {
if (count[i-1] > max) {
max = count[i-1];
}
}
return total + max;
}
return total;
}
Поскольку наш класс готов, мы можем подготовить несколько модульных тестов: один для проверки превышения лимита вызовов, а другой для проверки значения, возвращаемого с помощью нежадной стратегии:
public void nongreedyAlgorithmTest() {
NonGreedyAlgorithm nga = new NonGreedyAlgorithm(prepareNetwork(), 0);
Assertions.assertThrows(IllegalStateException.class, () -> {
nga.findMostFollowersPath("root");
});
}
public void nongreedyAlgorithmUnboundedTest() {
SocialConnector sc = prepareNetwork();
sc.switchCounter();
NonGreedyAlgorithm nga = new NonGreedyAlgorithm(sc, 0);
assertEquals(nga.findMostFollowersPath("root"), 6);
}
4. Результаты
Пришло время оценить нашу работу!
Сначала мы опробовали нашу жадную стратегию, проверив ее эффективность. Затем мы проверили ситуацию полным перебором, с ограничением API и без него.
Наша быстрая жадная процедура, которая каждый раз делает локально оптимальный выбор, возвращает числовое значение. С другой стороны, мы ничего не получаем от нежадного алгоритма из-за ограничения среды.
Сравнивая вывод двух методов, мы можем понять, как наша жадная стратегия спасла нас, даже если полученное значение не является оптимальным. Мы можем назвать это локальным оптимумом.
5. Вывод
В изменчивых и быстро меняющихся контекстах, таких как социальные сети, проблемы, требующие оптимального решения, могут стать ужасной химерой: труднодостижимой и в то же время нереалистичной.
Преодоление ограничений и оптимизация вызовов API — это отдельная тема, но, как мы уже говорили, жадные стратегии эффективны. Выбор такого подхода избавляет нас от многих проблем, давая взамен ценные результаты.
Имейте в виду, что не каждая ситуация подходит: нам нужно каждый раз оценивать наши обстоятельства.
Как всегда, пример кода из этого руководства доступен на GitHub .