1. Обзор
Задача о максимальном подмассиве — это задача найти ряд смежных элементов с максимальной суммой в любом заданном массиве.
Например, в приведенном ниже массиве выделенный подмассив имеет максимальную сумму (6):
В этом уроке мы рассмотрим два решения для поиска максимального подмассива в массиве . Один из них мы разработаем с O(n) временной и пространственной сложностью .
2. Алгоритм грубой силы
Грубая сила — это итеративный подход к решению проблемы. В большинстве случаев для решения требуется несколько итераций по структуре данных. В следующих нескольких разделах мы применим этот подход для решения задачи о максимальном подмассиве.
2.1. Подход
Вообще говоря, первое решение, которое приходит на ум, — вычислить сумму всех возможных подмассивов и вернуть тот, у которого сумма максимальна.
Для начала мы вычислим сумму всех подмассивов, начинающихся с индекса 0. И аналогичным образом мы найдем все подмассивы, начинающиеся с каждого индекса от 0 до n-1 , где n — длина массива:
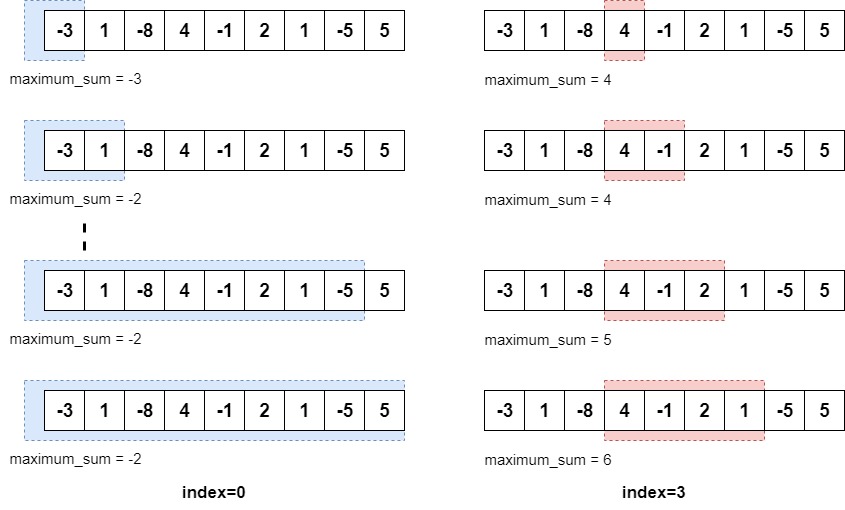
Итак, мы начнем с индекса 0 и добавим каждый элемент к текущей сумме в итерации. Мы также будем отслеживать максимальную сумму, увиденную до сих пор . Эта итерация показана в левой части изображения выше.
В правой части изображения мы видим итерацию, которая начинается с индекса 3 . В последней части этого изображения у нас есть подмассив с максимальной суммой между индексами 3 и 6 .
Однако наш алгоритм продолжит поиск всех подмассивов, начиная с индексов от 0 до n-1 .
2.2. Реализация
Давайте теперь посмотрим, как мы можем реализовать это решение на Java:
public int maxSubArray(int[] nums) {
int n = nums.length;
int maximumSubArraySum = Integer.MIN_VALUE;
int start = 0;
int end = 0;
for (int left = 0; left < n; left++) {
int runningWindowSum = 0;
for (int right = left; right < n; right++) {
runningWindowSum += nums[right];
if (runningWindowSum > maximumSubArraySum) {
maximumSubArraySum = runningWindowSum;
start = left;
end = right;
}
}
}
logger.info("Found Maximum Subarray between {} and {}", start, end);
return maximumSubArraySum;
}
Как и ожидалось, мы обновляем maxSubArraySum , если текущая сумма больше, чем предыдущая максимальная сумма. Примечательно, что затем мы также обновляем начало и конец , чтобы узнать расположение индексов этого подмассива .
2.3. Сложность
Вообще говоря, решение грубой силы многократно перебирает массив, чтобы получить все возможные решения. Это означает, что время, затрачиваемое этим решением, растет квадратично с количеством элементов в массиве. Это может не быть проблемой для массивов небольшого размера. Но по мере роста размера массива это решение становится неэффективным.
Изучив код, мы также можем увидеть, что есть два вложенных цикла for . Следовательно, мы можем сделать вывод, что временная сложность этого алгоритма составляет O(n 2 ) .
В последующих разделах мы решим эту задачу со сложностью O(n) с помощью динамического программирования.
3. Динамическое программирование
Динамическое программирование решает проблему, разделяя ее на более мелкие подзадачи. Это очень похоже на метод решения алгоритма «разделяй и властвуй». Однако основное отличие состоит в том, что динамическое программирование решает подзадачу только один раз.
Затем он сохраняет результат этой подзадачи и позже повторно использует этот результат для решения других связанных подзадач. Этот процесс известен как мемоизация .
3.1. Алгоритм Кадане
Алгоритм Кадане — популярное решение задачи о максимальном подмассиве, и это решение основано на динамическом программировании.
Наиболее важной задачей при решении задачи динамического программирования является поиск оптимальных подзадач .
3.2. Подход
Давайте поймем эту проблему по-другому:
На изображении выше мы предполагаем, что максимальный подмассив заканчивается в последнем местоположении индекса. Следовательно, максимальная сумма подмассива будет:
maximumSubArraySum = max_so_far + arr[n-1]
max_so_far — это максимальная сумма подмассива, который заканчивается на индексе n-2 . Это также показано на изображении выше.
Теперь мы можем применить это предположение к любому индексу в массиве. Например, максимальная сумма подмассива, которая заканчивается на n-2 , может быть рассчитана как:
maximumSubArraySum[n-2] = max_so_far[n-3] + arr[n-2]
Таким образом, мы можем сделать вывод, что:
maximumSubArraySum[i] = maximumSubArraySum[i-1] + arr[i]
Теперь, поскольку каждый элемент в массиве является специальным подмассивом размера один, нам также нужно проверить, больше ли элемент, чем сама максимальная сумма:
maximumSubArraySum[i] = Max(arr[i], maximumSubArraySum[i-1] + arr[i])
Глядя на эти уравнения, мы видим, что нам нужно найти максимальную сумму подмассива по каждому индексу массива. Таким образом, мы разбили нашу задачу на n подзадач. Мы можем найти максимальную сумму по каждому индексу, перебирая массив только один раз:

Выделенный элемент показывает текущий элемент в итерации. Для каждого индекса мы будем применять уравнение, полученное ранее, для вычисления значения max_ending_here . Это помогает нам определить , должны ли мы включать текущий элемент в подмассив или начинать новый подмассив, начиная с этого индекса .
Другая переменная, max_so_far , используется для хранения максимальной суммы подмассива, найденной во время итерации. Как только мы перейдем к последнему индексу, max_so_far сохранит сумму максимального подмассива.
3.3. Реализация
Опять же, давайте посмотрим, как теперь мы можем реализовать алгоритм Кадане в Java, следуя описанному выше подходу:
public int maxSubArraySum(int[] arr) {
int size = arr.length;
int start = 0;
int end = 0;
int maxSoFar = arr[0], maxEndingHere = arr[0];
for (int i = 1; i < size; i++) {
if (arr[i] > maxEndingHere + arr[i]) {
start = i;
maxEndingHere = arr[i];
} else
maxEndingHere = maxEndingHere + arr[i];
if (maxSoFar < maxEndingHere) {
maxSoFar = maxEndingHere;
end = i;
}
}
logger.info("Found Maximum Subarray between {} and {}", Math.min(start, end), end);
return maxSoFar;
}
Здесь мы обновили начало и конец , чтобы найти максимальные индексы подмассива.
Обратите внимание, что мы берем Math.min(start, end) вместо start в качестве начального индекса максимального подмассива. Это связано с тем, что если массив содержит только отрицательные числа, максимальный подмассив будет самым большим элементом. В этом случае if (arr[i] > maxEndingHere + arr[i]) всегда будет true . То есть значение start больше значения end.
3.4. Сложность
Поскольку нам нужно выполнить итерацию массива только один раз, временная сложность этого алгоритма составляет O(n) .
Итак, как мы видим, время, затрачиваемое этим решением, линейно растет с количеством элементов в массиве. Следовательно, он более эффективен, чем метод грубой силы, который мы обсуждали в предыдущем разделе.
4. Вывод
В этом кратком руководстве мы описали два способа решения проблемы максимального подмассива.
Во-первых, мы исследовали подход грубой силы и увидели, что это итеративное решение приводит к квадратичному времени. Позже мы обсудили алгоритм Кадане и использовали динамическое программирование для решения задачи за линейное время.
Как всегда, полный исходный код статьи доступен на GitHub .