1. Обзор
В этом руководстве мы рассмотрим, как реализовать кучу min-max в Java.
2. Мин-макс куча
Прежде всего, давайте посмотрим на определение и характеристики кучи. Минимальная куча — это полное бинарное дерево с признаками минимальной кучи и максимальной кучи:
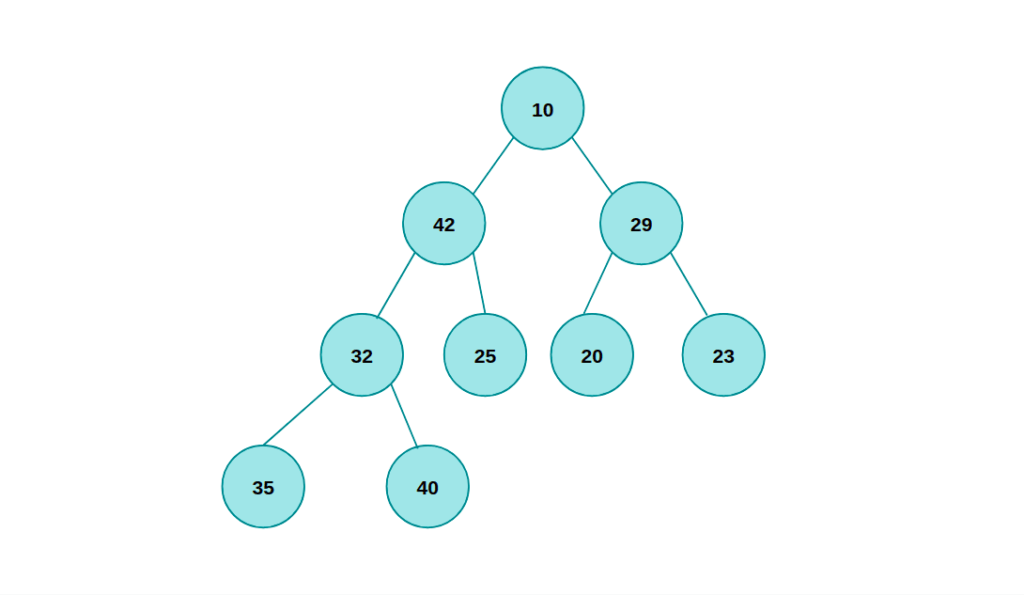
Как мы видим выше, каждый узел четного уровня дерева меньше всех своих потомков, а каждый узел нечетного уровня дерева больше всех своих потомков, где корень находится на нулевом уровне.
Каждый узел в куче min-max имеет элемент данных, который обычно называется ключом. Корень имеет наименьший ключ в куче min-max, а один из двух узлов на втором уровне является наибольшим ключом . Для каждого узла, такого как X , в куче min-max: ``
- Если
Xнаходится на минимальном (или даже) уровне, тоX.keyявляется минимальным ключом среди всех ключей в поддереве с корнемX. - Если
Xнаходится на максимальном (или нечетном) уровне, тоX.keyявляется максимальным ключом среди всех ключей в поддереве с корнемX.
Подобно min-heap или max-heap, вставка и удаление могут происходить с временной сложностью O (logN) .
3. Реализация на Java
Давайте начнем с простого класса, представляющего нашу минимальную кучу:
public class MinMaxHeap<T extends Comparable<T>> {
private List<T> array;
private int capacity;
private int indicator;
}
Как видно выше, мы используем индикатор для определения индекса последнего элемента, добавленного в массив. Но прежде чем мы продолжим, нам нужно помнить, что индекс массива начинается с нуля, но мы предполагаем, что индекс начинается с единицы в куче.
Мы можем найти индекс левого и правого детей, используя следующие методы:
private int getLeftChildIndex(int i) {
return 2 * i;
}
private int getRightChildIndex(int i) {
return ((2 * i) + 1);
}
Точно так же мы можем найти индекс родителя и прародителя элемента в массиве с помощью следующего кода:
private int getParentIndex(int i) {
return i / 2;
}
private int getGrandparentIndex(int i) {
return i / 4;
}
Теперь давайте продолжим работу над нашим простым классом минимальной и максимальной кучи:
public class MinMaxHeap<T extends Comparable<T>> {
private List<T> array;
private int capacity;
private int indicator;
MinMaxHeap(int capacity) {
array = new ArrayList<>();
this.capacity = capacity;
indicator = 1;
}
MinMaxHeap(List<T> array) {
this.array = array;
this.capacity = array.size();
this.indicator = array.size() + 1;
}
}
Здесь мы можем создать экземпляр кучи min-max двумя способами. Во- первых, мы инициируем массив с ArrayList и определенной емкостью, а во-вторых, мы делаем минимальную кучу из существующего массива.
Теперь давайте обсудим операции с нашей кучей.
3.1. Создавать
Давайте сначала рассмотрим создание кучи min-max из существующего массива. Здесь мы используем алгоритм Флойда с некоторой адаптацией, такой как алгоритм Heapify :
public List<T> create() {
for (int i = Math.floorDiv(array.size(), 2); i >= 1; i--) {
pushDown(array, i);
}
return array;
}
Давайте посмотрим, что именно произошло в приведенном выше коде, взглянув поближе на pushDown в следующем коде:
private void pushDown(List<T> array, int i) {
if (isEvenLevel(i)) {
pushDownMin(array, i);
} else {
pushDownMax(array, i);
}
}
Как видим, для всех четных уровней мы проверяем элементы массива с помощью pushDownMin. Этот алгоритм подобен heapify-down, который мы будем использовать для removeMin и removeMax :
private void pushDownMin(List<T> h, int i) {
while (getLeftChildIndex(i) < indicator) {
int indexOfSmallest = getIndexOfSmallestChildOrGrandChild(h, i);
//...
i = indexOfSmallest;
}
}
Во-первых, мы находим индекс наименьшего потомка или внука элемента ' i' . Далее действуем согласно следующим условиям.
Если наименьший дочерний элемент или внук не меньше текущего элемента, мы ломаемся. Другими словами, текущее расположение элементов похоже на min-heap:
if (h.get(indexOfSmallest - 1).compareTo(h.get(i - 1)) < 0) {
//...
} else {
break;
}
Если наименьший дочерний или внучатый элемент меньше текущего элемента, мы меняем его местами с его родителем или прародителем:
if (getParentIndex(getParentIndex(indexOfSmallest)) == i) {
if (h.get(indexOfSmallest - 1).compareTo(h.get(i - 1)) < 0) {
swap(indexOfSmallest - 1, i - 1, h);
if (h.get(indexOfSmallest - 1)
.compareTo(h.get(getParentIndex(indexOfSmallest) - 1)) > 0) {
swap(indexOfSmallest - 1, getParentIndex(indexOfSmallest) - 1, h);
}
}
} else if (h.get(indexOfSmallest - 1).compareTo(h.get(i - 1)) < 0) {
swap(indexOfSmallest - 1, i - 1, h);
}
Мы продолжим описанные выше операции, пока не найдем дочерний элемент для элемента «i».
Теперь давайте посмотрим, как работает getIndexOfSmallestChildOrGrandChild . Это довольно легко! Во-первых, мы предполагаем, что левый дочерний элемент имеет наименьшее значение, а затем сравниваем его с другими:
private int getIndexOfSmallestChildOrGrandChild(List<T> h, int i) {
int minIndex = getLeftChildIndex(i);
T minValue = h.get(minIndex - 1);
// rest of the implementation
}
На каждом шаге, если индекс больше индикатора, ответом является последнее найденное минимальное значение.
Например, давайте сравним min-value с правым дочерним элементом:
if (getRightChildIndex(i) < indicator) {
if (h.get(getRightChildIndex(i) - 1).compareTo(minValue) < 0) {
minValue = h.get(getRightChildIndex(i));
minIndex = getRightChildIndex(i);
}
} else {
return minIndex;
}
Теперь давайте создадим тест, чтобы убедиться, что создание кучи min-max из неупорядоченного массива работает нормально:
@Test
public void givenUnOrderedArray_WhenCreateMinMaxHeap_ThenIsEqualWithMinMaxHeapOrdered() {
List<Integer> list = Arrays.asList(34, 12, 28, 9, 30, 19, 1, 40);
MinMaxHeap<Integer> minMaxHeap = new MinMaxHeap<>(list);
minMaxHeap.create();
Assert.assertEquals(List.of(1, 40, 34, 9, 30, 19, 28, 12), list);
}
Алгоритм для pushDownMax идентичен алгоритму для pushDownMin , но при всех сравнениях операторы меняются местами.
3.2. Вставлять
Давайте посмотрим, как добавить элемент в кучу min-max:
public void insert(T item) {
if (isEmpty()) {
array.add(item);
indicator++;
} else if (!isFull()) {
array.add(item);
pushUp(array, indicator);
indicator++;
} else {
throw new RuntimeException("invalid operation !!!");
}
}
Во-первых, мы проверяем, пуста куча или нет. Если куча пуста, добавляем новый элемент и увеличиваем показатель. В противном случае добавленный новый элемент может изменить порядок кучи min-max, поэтому нам нужно настроить кучу с помощью pushUp :
private void pushUp(List<T>h,int i) {
if (i != 1) {
if (isEvenLevel(i)) {
if (h.get(i - 1).compareTo(h.get(getParentIndex(i) - 1)) < 0) {
pushUpMin(h, i);
} else {
swap(i - 1, getParentIndex(i) - 1, h);
i = getParentIndex(i);
pushUpMax(h, i);
}
} else if (h.get(i - 1).compareTo(h.get(getParentIndex(i) - 1)) > 0) {
pushUpMax(h, i);
} else {
swap(i - 1, getParentIndex(i) - 1, h);
i = getParentIndex(i);
pushUpMin(h, i);
}
}
}
Как мы видим выше, новый элемент сравнивает своего родителя, затем:
- Если обнаружено, что он меньше (больше), чем родитель, то он определенно меньше (больше), чем все остальные элементы на максимальных (минимальных) уровнях, которые находятся на пути к корню кучи.
- Путь от нового элемента к корню (учитывая только минимальные/максимальные уровни) должен быть в порядке убывания (возрастания), как это было до вставки. Итак, нам нужно сделать бинарную вставку нового элемента в эту последовательность
Теперь давайте посмотрим на pushUpMin следующим образом:
private void pushUpMin(List<T> h , int i) {
while(hasGrandparent(i) && h.get(i - 1)
.compareTo(h.get(getGrandparentIndex(i) - 1)) < 0) {
swap(i - 1, getGrandparentIndex(i) - 1, h);
i = getGrandparentIndex(i);
}
}
Технически проще поменять местами новый элемент с его родителем, пока родитель больше. Кроме того, pushUpMax идентичен pushUpMin , но при всех сравнениях операторы меняются местами.
Теперь давайте создадим тест, чтобы убедиться, что вставка нового элемента в кучу min-max работает нормально:
@Test
public void givenNewElement_WhenInserted_ThenIsEqualWithMinMaxHeapOrdered() {
MinMaxHeap<Integer> minMaxHeap = new MinMaxHeap(8);
minMaxHeap.insert(34);
minMaxHeap.insert(12);
minMaxHeap.insert(28);
minMaxHeap.insert(9);
minMaxHeap.insert(30);
minMaxHeap.insert(19);
minMaxHeap.insert(1);
minMaxHeap.insert(40);
Assert.assertEquals(List.of(1, 40, 28, 12, 30, 19, 9, 34),
minMaxHeap.getMinMaxHeap());
}
3.3. Найти мин.
Основной элемент в куче min-max всегда находится в корне, поэтому мы можем найти его за временную сложность O(1):
public T min() {
if (!isEmpty()) {
return array.get(0);
}
return null;
}
3.4. Найдите Макса
Максимальный элемент в куче min-max всегда находится на первом нечетном уровне, поэтому мы можем найти его за временную сложность O (1) с помощью простого сравнения:
public T max() {
if (!isEmpty()) {
if (indicator == 2) {
return array.get(0);
}
if (indicator == 3) {
return array.get(1);
}
return array.get(1).compareTo(array.get(2)) < 0 ? array.get(2) : array.get(1);
}
return null;
}
3.5. Удалить мин.
В этом случае мы найдем элемент min, а затем заменим его последним элементом массива:
public T removeMin() {
T min = min();
if (min != null) {
if (indicator == 2) {
array.remove(indicator--);
return min;
}
array.set(0, array.get(--indicator - 1));
array.remove(indicator - 1);
pushDown(array, 1);
}
return min;
}
3.6. Удалить Макс
Удаление элемента max аналогично удалению min, с той лишь разницей, что мы находим индекс элемента max, а затем вызываем pushDown :
public T removeMax() {
T max = max();
if (max != null) {
int maxIndex;
if (indicator == 2) {
maxIndex = 0;
array.remove(--indicator - 1);
return max;
} else if (indicator == 3) {
maxIndex = 1;
array.remove(--indicator - 1);
return max;
} else {
maxIndex = array.get(1).compareTo(array.get(2)) < 0 ? 2 : 1;
}
array.set(maxIndex, array.get(--indicator - 1));
array.remove(indicator - 1);
pushDown(array, maxIndex + 1);
}
return max;
}
4. Вывод
В этом руководстве мы рассмотрели реализацию кучи min-max в Java и изучили некоторые из наиболее распространенных операций.
Во-первых, мы узнали, что такое куча min-max, включая некоторые из наиболее распространенных функций. Затем мы увидели, как создавать, вставлять, находить-минимум, находить-макс, удалять-минимум и удалять-макс элементы в нашей реализации кучи min-max.
Как обычно, все примеры, использованные в этой статье, доступны на GitHub .