1. Обзор
В этой статье мы собираемся изучить алгоритм поиска по дереву Монте-Карло (MCTS) и его приложения.
Мы подробно рассмотрим его этапы, реализовав игру «Крестики-нолики» на Java . Мы разработаем общее решение, которое можно будет использовать во многих других практических приложениях с минимальными изменениями.
2. Введение
Проще говоря, поиск по дереву Монте-Карло — это алгоритм вероятностного поиска. Это уникальный алгоритм принятия решений из-за его эффективности в открытых средах с огромным количеством возможностей.
Если вы уже знакомы с алгоритмами теории игр, такими как Minimax , вам потребуется функция для оценки текущего состояния, и она должна вычислить множество уровней в дереве игры, чтобы найти оптимальный ход.
К сожалению, это невозможно сделать в такой игре, как го , в которой есть высокий коэффициент ветвления (что приводит к миллионам возможностей по мере увеличения высоты дерева), и трудно написать хорошую функцию оценки, чтобы вычислить, насколько хороша ветвь. текущее состояние.
Поиск по дереву Монте-Карло применяет метод Монте-Карло к поиску по дереву игры. Поскольку он основан на случайной выборке игровых состояний, ему не нужно перебирать каждую возможность методом грубой силы. Кроме того, это не обязательно требует от нас написания оценки или хороших эвристических функций.
И короткое замечание: он произвел революцию в мире компьютерного го. С марта 2016 года он стал широко распространенной темой исследований, поскольку Google AlphaGo (построенный с помощью MCTS и нейронной сети) победил Ли Седоля (чемпион мира по го).
3. Алгоритм поиска по дереву Монте-Карло
Теперь давайте рассмотрим, как работает алгоритм. Сначала мы построим предварительное дерево (игровое дерево) с корневым узлом, а затем будем расширять его случайными развертываниями. В процессе мы будем поддерживать количество посещений и количество побед для каждого узла.
В конце мы собираемся выбрать узел с наиболее многообещающей статистикой.
Алгоритм состоит из четырех этапов; давайте подробно рассмотрим их все.
3.1. Выбор
На этом начальном этапе алгоритм начинает с корневого узла и выбирает дочерний узел таким образом, чтобы выбрать узел с максимальным коэффициентом выигрыша. Мы также хотим убедиться, что каждому узлу предоставлен равный шанс.
Идея состоит в том, чтобы продолжать выбирать оптимальные дочерние узлы, пока мы не достигнем конечного узла дерева. Хороший способ выбрать такой дочерний узел — использовать формулу UCT (верхняя доверительная граница, применяемая к деревьям)
:
wi= количество побед послеi-го ходаni= количество симуляций послеi-го ходаc= параметр разведки (теоретически равен √2)t= общее количество симуляций для родительского узла
Формула гарантирует, что ни одно государство не станет жертвой голода, а также чаще, чем их коллеги, играет в многообещающие отрасли.
3.2. Расширение
Когда он больше не может применять UCT для поиска узла-преемника, он расширяет игровое дерево, добавляя все возможные состояния из конечного узла.
3.3. Моделирование
После расширения алгоритм произвольно выбирает дочерний узел и моделирует рандомизированную игру из выбранного узла, пока не достигнет результирующего состояния игры. Если узлы выбираются случайным или полуслучайным образом во время воспроизведения, это называется легким воспроизведением. Вы также можете выбрать тяжелую игру, написав эвристики качества или функции оценки.
3.4. Обратное распространение
Это также известно как фаза обновления. Как только алгоритм достигает конца игры, он оценивает состояние, чтобы выяснить, кто из игроков выиграл. Он проходит вверх к корню и увеличивает показатель посещения для всех посещенных узлов. Он также обновляет счет выигрыша для каждого узла, если игрок на этой позиции выиграл игру.
MCTS продолжает повторять эти четыре фазы до определенного фиксированного количества итераций или определенного фиксированного периода времени.
В этом подходе мы оцениваем выигрышный счет для каждого узла на основе случайных ходов. Таким образом, чем выше количество итераций, тем надежнее становится оценка. Оценки алгоритма будут менее точными в начале поиска и продолжат улучшаться по прошествии достаточного количества времени. Опять же, это зависит исключительно от типа проблемы.
4. Пробный прогон
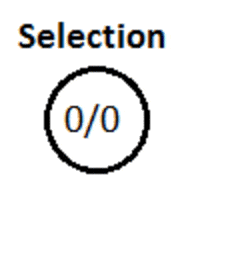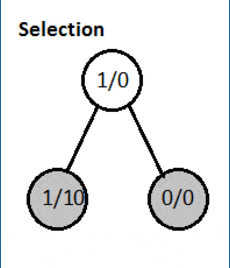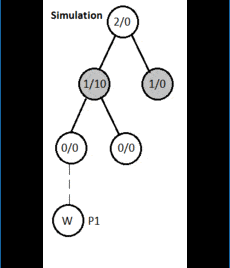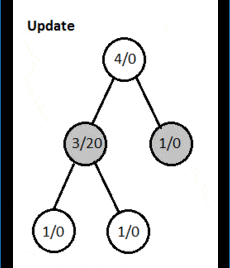
Здесь узлы содержат статистику в виде общего числа посещений/счета выигрышей.
5. Реализация
Теперь давайте реализуем игру в крестики-нолики, используя алгоритм поиска по дереву Монте-Карло.
Мы разработаем универсальное решение для MCTS, которое можно будет использовать и для многих других настольных игр. Мы рассмотрим большую часть кода в самой статье.
Хотя, чтобы сделать объяснение четким, нам, возможно, придется пропустить некоторые незначительные детали (не особенно связанные с MCTS), но вы всегда можете найти полную реализацию здесь .
Прежде всего, нам нужна базовая реализация для классов Tree и Node , чтобы иметь функциональность поиска по дереву:
public class Node {
State state;
Node parent;
List<Node> childArray;
// setters and getters
}
public class Tree {
Node root;
}
Поскольку каждый узел будет иметь определенное состояние проблемы, давайте также реализуем класс State :
public class State {
Board board;
int playerNo;
int visitCount;
double winScore;
// copy constructor, getters, and setters
public List<State> getAllPossibleStates() {
// constructs a list of all possible states from current state
}
public void randomPlay() {
/* get a list of all possible positions on the board and
play a random move */
}
}
Теперь давайте реализуем класс MonteCarloTreeSearch , который будет отвечать за поиск следующего лучшего хода из заданной игровой позиции:
public class MonteCarloTreeSearch {
static final int WIN_SCORE = 10;
int level;
int opponent;
public Board findNextMove(Board board, int playerNo) {
// define an end time which will act as a terminating condition
opponent = 3 - playerNo;
Tree tree = new Tree();
Node rootNode = tree.getRoot();
rootNode.getState().setBoard(board);
rootNode.getState().setPlayerNo(opponent);
while (System.currentTimeMillis() < end) {
Node promisingNode = selectPromisingNode(rootNode);
if (promisingNode.getState().getBoard().checkStatus()
== Board.IN_PROGRESS) {
expandNode(promisingNode);
}
Node nodeToExplore = promisingNode;
if (promisingNode.getChildArray().size() > 0) {
nodeToExplore = promisingNode.getRandomChildNode();
}
int playoutResult = simulateRandomPlayout(nodeToExplore);
backPropogation(nodeToExplore, playoutResult);
}
Node winnerNode = rootNode.getChildWithMaxScore();
tree.setRoot(winnerNode);
return winnerNode.getState().getBoard();
}
}
Здесь мы продолжаем повторять все четыре фазы до заранее определенного времени, и в конце мы получаем дерево с надежной статистикой для принятия разумного решения.
Теперь давайте реализуем методы для всех фаз.
Мы начнем с этапа выбора , который также требует внедрения UCT:
private Node selectPromisingNode(Node rootNode) {
Node node = rootNode;
while (node.getChildArray().size() != 0) {
node = UCT.findBestNodeWithUCT(node);
}
return node;
}
public class UCT {
public static double uctValue(
int totalVisit, double nodeWinScore, int nodeVisit) {
if (nodeVisit == 0) {
return Integer.MAX_VALUE;
}
return ((double) nodeWinScore / (double) nodeVisit)
+ 1.41 * Math.sqrt(Math.log(totalVisit) / (double) nodeVisit);
}
public static Node findBestNodeWithUCT(Node node) {
int parentVisit = node.getState().getVisitCount();
return Collections.max(
node.getChildArray(),
Comparator.comparing(c -> uctValue(parentVisit,
c.getState().getWinScore(), c.getState().getVisitCount())));
}
}
На этом этапе рекомендуется конечный узел, который следует расширить на этапе расширения:
private void expandNode(Node node) {
List<State> possibleStates = node.getState().getAllPossibleStates();
possibleStates.forEach(state -> {
Node newNode = new Node(state);
newNode.setParent(node);
newNode.getState().setPlayerNo(node.getState().getOpponent());
node.getChildArray().add(newNode);
});
}
Затем мы пишем код для выбора случайного узла и имитации случайного воспроизведения из него. Кроме того, у нас будет функция обновления для распространения оценки и количества посещений, начиная с листа к корню:
private void backPropogation(Node nodeToExplore, int playerNo) {
Node tempNode = nodeToExplore;
while (tempNode != null) {
tempNode.getState().incrementVisit();
if (tempNode.getState().getPlayerNo() == playerNo) {
tempNode.getState().addScore(WIN_SCORE);
}
tempNode = tempNode.getParent();
}
}
private int simulateRandomPlayout(Node node) {
Node tempNode = new Node(node);
State tempState = tempNode.getState();
int boardStatus = tempState.getBoard().checkStatus();
if (boardStatus == opponent) {
tempNode.getParent().getState().setWinScore(Integer.MIN_VALUE);
return boardStatus;
}
while (boardStatus == Board.IN_PROGRESS) {
tempState.togglePlayer();
tempState.randomPlay();
boardStatus = tempState.getBoard().checkStatus();
}
return boardStatus;
}
Теперь мы закончили с реализацией MCTS. Все, что нам нужно, — это конкретная реализация класса Board в крестиках-ноликах . Обратите внимание, что для того, чтобы играть в другие игры с нашей реализацией; Нам просто нужно изменить класс Board .
public class Board {
int[][] boardValues;
public static final int DEFAULT_BOARD_SIZE = 3;
public static final int IN_PROGRESS = -1;
public static final int DRAW = 0;
public static final int P1 = 1;
public static final int P2 = 2;
// getters and setters
public void performMove(int player, Position p) {
this.totalMoves++;
boardValues[p.getX()][p.getY()] = player;
}
public int checkStatus() {
/* Evaluate whether the game is won and return winner.
If it is draw return 0 else return -1 */
}
public List<Position> getEmptyPositions() {
int size = this.boardValues.length;
List<Position> emptyPositions = new ArrayList<>();
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
if (boardValues[i][j] == 0)
emptyPositions.add(new Position(i, j));
}
}
return emptyPositions;
}
}
Мы только что внедрили ИИ, который невозможно победить в крестиках-ноликах. Давайте напишем единичный случай, который демонстрирует, что ИИ против ИИ всегда приводит к ничьей:
@Test
public void givenEmptyBoard_whenSimulateInterAIPlay_thenGameDraw() {
Board board = new Board();
int player = Board.P1;
int totalMoves = Board.DEFAULT_BOARD_SIZE * Board.DEFAULT_BOARD_SIZE;
for (int i = 0; i < totalMoves; i++) {
board = mcts.findNextMove(board, player);
if (board.checkStatus() != -1) {
break;
}
player = 3 - player;
}
int winStatus = board.checkStatus();
assertEquals(winStatus, Board.DRAW);
}
6. Преимущества
- Это не обязательно требует каких-либо тактических знаний об игре.
- Обычная реализация MCTS может быть повторно использована для любого количества игр с небольшими изменениями.
- Сосредоточен на узлах с более высокими шансами на победу в игре.
- Подходит для задач с высоким коэффициентом ветвления, поскольку не тратит вычисления на все возможные ветвления.
- Алгоритм очень прост в реализации
- Выполнение может быть остановлено в любой момент времени, и оно по-прежнему будет предлагать следующее лучшее состояние, вычисленное на данный момент.
7. Недостаток
Если MCTS используется в своей базовой форме без каких-либо улучшений, он может не предложить разумных действий. Это может произойти, если узлы не посещаются должным образом, что приводит к неточным оценкам.
Однако MCTS можно улучшить с помощью некоторых методов. Он включает в себя методы, специфичные для предметной области, а также независимые от предметной области методы.
В методах, специфичных для предметной области, этап моделирования обеспечивает более реалистичное воспроизведение, чем стохастическое моделирование. Хотя это требует знания конкретных игровых техник и правил.
8. Резюме
На первый взгляд трудно поверить, что алгоритм, основанный на случайном выборе, может привести к умному ИИ. Однако продуманная реализация MCTS действительно может предоставить нам решение, которое можно использовать во многих играх, а также в задачах принятия решений.
Как всегда, полный код алгоритма можно найти на GitHub .