1. Обзор
В этом руководстве мы рассмотрим концепцию сопоставления строк с образцом и то, как мы можем сделать это быстрее. Затем мы рассмотрим его реализацию на Java.
2. Сопоставление строк с образцом
2.1. Определение
В строках сопоставление с образцом — это процесс проверки заданной последовательности символов, называемой шаблоном, в последовательности символов, называемой текстом .
Основные ожидания от сопоставления с шаблоном, когда шаблон не является регулярным выражением:
- совпадение должно быть точным, а не частичным
- результат должен содержать все совпадения, а не только первое совпадение
- результат должен содержать позицию каждого совпадения в тексте
2.2. Поиск шаблона
Давайте используем пример, чтобы понять простую задачу сопоставления с образцом:
Pattern: NA
Text: HAVANABANANA
Match1: ----NA------
Match2: --------NA--
Match3: ----------NA
Мы видим, что паттерн NA встречается в тексте трижды. Чтобы получить этот результат, мы можем подумать о перемещении шаблона вниз по тексту по одному символу за раз и проверке совпадения.
Однако это метод грубой силы с временной сложностью O(p*t) , где p — длина шаблона, а t — длина текста.
Предположим, у нас есть более одного шаблона для поиска. Затем временная сложность также увеличивается линейно, поскольку для каждого шаблона потребуется отдельная итерация.
2.3. Попробуйте структуру данных для хранения шаблонов
Мы можем сократить время поиска, сохранив шаблоны в структуре данных trie , которая известна своим быстрым поиском элементов.
Мы знаем, что структура данных trie хранит символы строки в древовидной структуре. Итак, для двух строк {NA, NAB} мы получим дерево с двумя путями:
Создание дерева позволяет перемещать группу шаблонов вниз по тексту и проверять совпадения всего за одну итерацию.
Обратите внимание, что мы используем символ $ для обозначения конца строки.
2.4. Структура данных Suffix Trie для хранения текста
Суффикс trie , с другой стороны, представляет собой структуру данных trie, построенную с использованием всех возможных суффиксов одной строки .
Для предыдущего примера HAVANABANANA мы можем построить суффиксное дерево:

Попытки суффикса создаются для текста и обычно выполняются как часть этапа предварительной обработки. После этого можно быстро выполнить поиск шаблонов, найдя путь, соответствующий последовательности шаблонов.
Однако известно, что дерево суффиксов занимает много места, поскольку каждый символ строки хранится в ребре.
В следующем разделе мы рассмотрим улучшенную версию суффиксного дерева.
3. Суффиксное дерево
Суффиксное дерево — это просто сжатое суффиксное дерево . Это означает, что, соединяя ребра, мы можем хранить группу символов и тем самым значительно уменьшать объем памяти.
Итак, мы можем создать дерево суффиксов для того же текста HAVANABANANA :
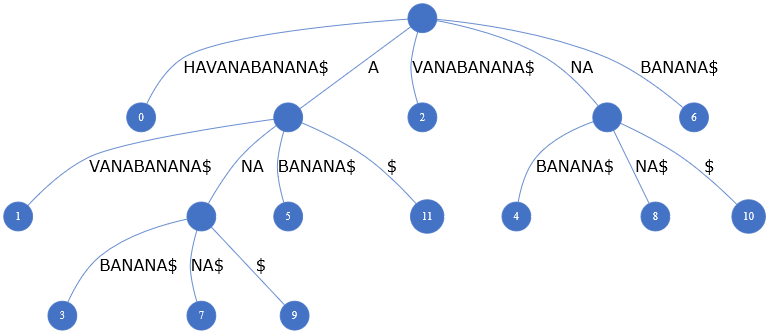
Каждый путь, начинающийся от корня к листу, представляет собой суффикс строки HAVANABANANA .
Дерево суффиксов также хранит положение суффикса в листовом узле . Например, BANANA$ — это суффикс, начинающийся с седьмой позиции. Следовательно, его значение будет равно шести с использованием нумерации, начинающейся с нуля. Точно так же A->BANANA$ — это еще один суффикс, начинающийся с пятой позиции, как мы видим на картинке выше.
Итак, посмотрев на вещи в перспективе, мы можем видеть, что совпадение с шаблоном происходит, когда мы можем получить путь, начинающийся от корневого узла с ребрами, полностью совпадающими с заданным шаблоном позиционно .
Если путь заканчивается на листовом узле, мы получаем совпадение суффикса. В противном случае мы получим просто совпадение подстроки. Например, шаблон NA является суффиксом HAVANABANA[NA] и подстрокой HAVA[NA]BANANA .
В следующем разделе мы увидим, как реализовать эту структуру данных в Java.
4. Структура данных
Давайте создадим структуру данных дерева суффиксов. Нам понадобятся два класса домена.
Во- первых, нам нужен класс для представления узла дерева . Он должен хранить ребра дерева и его дочерние узлы. Кроме того, когда это конечный узел, ему необходимо хранить позиционное значение суффикса.
Итак, давайте создадим наш класс Node :
public class Node {
private String text;
private List<Node> children;
private int position;
public Node(String word, int position) {
this.text = word;
this.position = position;
this.children = new ArrayList<>();
}
// getters, setters, toString()
}
Во- вторых, нам нужен класс для представления дерева и хранения корневого узла . Он также должен хранить полный текст, из которого генерируются суффиксы.
Следовательно, у нас есть класс SuffixTree :
public class SuffixTree {
private static final String WORD_TERMINATION = "$";
private static final int POSITION_UNDEFINED = -1;
private Node root;
private String fullText;
public SuffixTree(String text) {
root = new Node("", POSITION_UNDEFINED);
fullText = text;
}
}
5. Вспомогательные методы для добавления данных
Прежде чем мы напишем нашу основную логику для хранения данных, давайте добавим несколько вспомогательных методов. Они пригодятся позже.
Давайте изменим наш класс SuffixTree , чтобы добавить некоторые методы, необходимые для построения дерева.
5.1. Добавление дочернего узла
Во-первых, давайте создадим метод addChildNode для добавления нового дочернего узла к любому заданному родительскому узлу :
private void addChildNode(Node parentNode, String text, int index) {
parentNode.getChildren().add(new Node(text, index));
}
5.2. Поиск самого длинного общего префикса двух строк
Во- вторых, мы напишем простой служебный метод getLongestCommonPrefix для поиска самого длинного общего префикса двух строк :
private String getLongestCommonPrefix(String str1, String str2) {
int compareLength = Math.min(str1.length(), str2.length());
for (int i = 0; i < compareLength; i++) {
if (str1.charAt(i) != str2.charAt(i)) {
return str1.substring(0, i);
}
}
return str1.substring(0, compareLength);
}
5.3. Разделение узла
В-третьих, у нас есть метод для выделения дочернего узла из заданного родителя . В этом процессе текстовое значение родительского узла будет усечено, а усеченная справа строка станет текстовым значением дочернего узла. Кроме того, дочерние узлы родителя будут переданы дочернему узлу.
На рисунке ниже видно, что ANA разделяется на A->NA. После этого новый суффикс ABANANA$ можно добавить как A->BANANA$ :
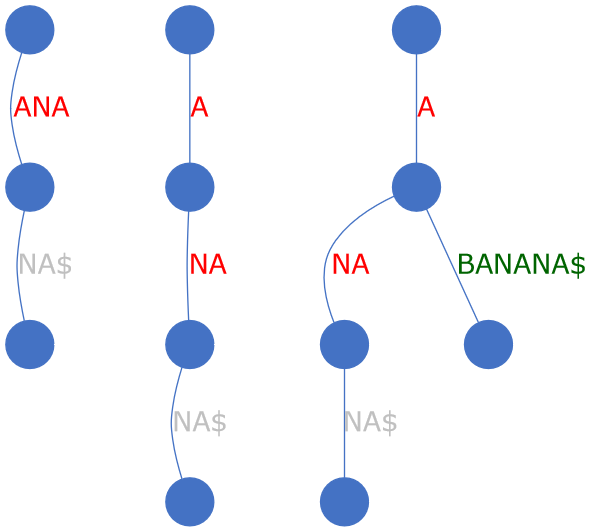
Короче говоря, это удобный метод, который пригодится при вставке нового узла:
private void splitNodeToParentAndChild(Node parentNode, String parentNewText, String childNewText) {
Node childNode = new Node(childNewText, parentNode.getPosition());
if (parentNode.getChildren().size() > 0) {
while (parentNode.getChildren().size() > 0) {
childNode.getChildren()
.add(parentNode.getChildren().remove(0));
}
}
parentNode.getChildren().add(childNode);
parentNode.setText(parentNewText);
parentNode.setPosition(POSITION_UNDEFINED);
}
6. Вспомогательный метод обхода
Давайте теперь создадим логику для обхода дерева. Мы будем использовать этот метод как для построения дерева, так и для поиска шаблонов.
6.1. Частичное совпадение против полного совпадения
Во-первых, давайте разберемся с понятием частичного совпадения и полного совпадения, рассмотрев дерево, заполненное несколькими суффиксами:
Чтобы добавить новый суффикс ANABANANA$ , мы проверяем, существует ли какой-либо узел, который можно изменить или расширить для размещения нового значения. Для этого мы сравниваем новый текст со всеми узлами и обнаруживаем, что существующий узел [A]VANABANANA$ совпадает по первому символу. Итак, это узел, который нам нужно изменить, и это совпадение можно назвать частичным совпадением.
С другой стороны, предположим, что мы ищем паттерн VANE на том же дереве. Мы знаем, что он частично совпадает с [VAN]ABANANA$ по первым трем символам. Если бы все четыре символа совпали, мы могли бы назвать это полным совпадением. Для поиска по шаблону необходимо полное совпадение .
Подводя итог, мы будем использовать частичное совпадение при построении дерева и полное совпадение при поиске шаблонов. Мы будем использовать флаг isAllowPartialMatch , чтобы указать тип совпадения, который нам нужен в каждом случае.
6.2. Обход дерева
Теперь давайте напишем нашу логику для обхода дерева, если мы можем позиционно сопоставить заданный шаблон:
List<Node> getAllNodesInTraversePath(String pattern, Node startNode, boolean isAllowPartialMatch) {
// ...
}
Мы будем вызывать это рекурсивно и возвращать список всех узлов , которые мы найдем на нашем пути .
Начнем со сравнения первого символа текста шаблона с текстом узла:
if (pattern.charAt(0) == nodeText.charAt(0)) {
// logic to handle remaining characters
}
Для частичного совпадения, если шаблон короче или равен по длине тексту узла, мы добавляем текущий узел в наш список узлов и останавливаемся здесь:
if (isAllowPartialMatch && pattern.length() <= nodeText.length()) {
nodes.add(currentNode);
return nodes;
}
Затем мы сравниваем оставшиеся символы текста этого узла с символами шаблона. Если шаблон имеет позиционное несоответствие с текстом узла, мы останавливаемся здесь. Текущий узел включается в список узлов только при частичном совпадении:
int compareLength = Math.min(nodeText.length(), pattern.length());
for (int j = 1; j < compareLength; j++) {
if (pattern.charAt(j) != nodeText.charAt(j)) {
if (isAllowPartialMatch) {
nodes.add(currentNode);
}
return nodes;
}
}
Если шаблон соответствует тексту узла, мы добавляем текущий узел в наш список узлов :
nodes.add(currentNode);
Но если в шаблоне больше символов, чем в тексте узла, нам нужно проверить дочерние узлы. Для этого мы делаем рекурсивный вызов, передавая currentNode в качестве начального узла и оставшуюся часть шаблона в качестве нового шаблона. Список узлов, возвращаемый этим вызовом, добавляется к нашему списку узлов , если он не пуст. Если он пуст для сценария полного совпадения, это означает, что имело место несоответствие, поэтому, чтобы указать это, мы добавляем нулевой элемент. И мы возвращаем узлы :
if (pattern.length() > compareLength) {
List nodes2 = getAllNodesInTraversePath(pattern.substring(compareLength), currentNode,
isAllowPartialMatch);
if (nodes2.size() > 0) {
nodes.addAll(nodes2);
} else if (!isAllowPartialMatch) {
nodes.add(null);
}
}
return nodes;
Собрав все это вместе, давайте создадим getAllNodesInTraversePath :
private List<Node> getAllNodesInTraversePath(String pattern, Node startNode, boolean isAllowPartialMatch) {
List<Node> nodes = new ArrayList<>();
for (int i = 0; i < startNode.getChildren().size(); i++) {
Node currentNode = startNode.getChildren().get(i);
String nodeText = currentNode.getText();
if (pattern.charAt(0) == nodeText.charAt(0)) {
if (isAllowPartialMatch && pattern.length() <= nodeText.length()) {
nodes.add(currentNode);
return nodes;
}
int compareLength = Math.min(nodeText.length(), pattern.length());
for (int j = 1; j < compareLength; j++) {
if (pattern.charAt(j) != nodeText.charAt(j)) {
if (isAllowPartialMatch) {
nodes.add(currentNode);
}
return nodes;
}
}
nodes.add(currentNode);
if (pattern.length() > compareLength) {
List<Node> nodes2 = getAllNodesInTraversePath(pattern.substring(compareLength),
currentNode, isAllowPartialMatch);
if (nodes2.size() > 0) {
nodes.addAll(nodes2);
} else if (!isAllowPartialMatch) {
nodes.add(null);
}
}
return nodes;
}
}
return nodes;
}
7. Алгоритм
7.1. Хранение данных
Теперь мы можем написать нашу логику для хранения данных. Начнем с определения нового метода addSuffix в классе SuffixTree :
private void addSuffix(String suffix, int position) {
// ...
}
Вызывающая сторона предоставит позицию суффикса.
Далее давайте напишем логику для обработки суффикса. Во-первых, нам нужно проверить, существует ли путь, соответствующий суффиксу, хотя бы частично, вызвав наш вспомогательный метод getAllNodesInTraversePath с isAllowPartialMatch , установленным как true . Если пути не существует, мы можем добавить наш суффикс как дочерний к корню:
List<Node> nodes = getAllNodesInTraversePath(pattern, root, true);
if (nodes.size() == 0) {
addChildNode(root, suffix, position);
}
Однако, если путь существует, это означает, что нам нужно изменить существующий узел . Этот узел будет последним в списке узлов . Нам также нужно выяснить, каким должен быть новый текст для этого существующего узла. Если в списке узлов только один элемент, то используется суффикс . В противном случае мы исключаем общий префикс до последнего узла из суффикса , чтобы получить новый текст :
Node lastNode = nodes.remove(nodes.size() - 1);
String newText = suffix;
if (nodes.size() > 0) {
String existingSuffixUptoLastNode = nodes.stream()
.map(a -> a.getText())
.reduce("", String::concat);
newText = newText.substring(existingSuffixUptoLastNode.length());
}
Для изменения существующего узла давайте создадим новый метод extendNode, который мы будем вызывать с того места, где мы остановились в методе addSuffix . Этот метод имеет две ключевые обязанности. Один из них — разбить существующий узел на родительский и дочерний, а другой — добавить дочерний узел к вновь созданному родительскому узлу. Мы разбиваем родительский узел только для того, чтобы сделать его общим узлом для всех его дочерних узлов. Итак, наш новый метод готов:
private void extendNode(Node node, String newText, int position) {
String currentText = node.getText();
String commonPrefix = getLongestCommonPrefix(currentText, newText);
if (commonPrefix != currentText) {
String parentText = currentText.substring(0, commonPrefix.length());
String childText = currentText.substring(commonPrefix.length());
splitNodeToParentAndChild(node, parentText, childText);
}
String remainingText = newText.substring(commonPrefix.length());
addChildNode(node, remainingText, position);
}
Теперь мы можем вернуться к нашему методу добавления суффикса, в котором теперь есть вся логика:
private void addSuffix(String suffix, int position) {
List<Node> nodes = getAllNodesInTraversePath(suffix, root, true);
if (nodes.size() == 0) {
addChildNode(root, suffix, position);
} else {
Node lastNode = nodes.remove(nodes.size() - 1);
String newText = suffix;
if (nodes.size() > 0) {
String existingSuffixUptoLastNode = nodes.stream()
.map(a -> a.getText())
.reduce("", String::concat);
newText = newText.substring(existingSuffixUptoLastNode.length());
}
extendNode(lastNode, newText, position);
}
}
Наконец, давайте изменим наш конструктор SuffixTree для генерации суффиксов и вызовем наш предыдущий метод addSuffix для итеративного добавления их в нашу структуру данных:
public void SuffixTree(String text) {
root = new Node("", POSITION_UNDEFINED);
for (int i = 0; i < text.length(); i++) {
addSuffix(text.substring(i) + WORD_TERMINATION, i);
}
fullText = text;
}
7.2. Поиск данных
Определив нашу древовидную структуру суффиксов для хранения данных, теперь мы можем написать логику для выполнения нашего поиска .
Мы начнем с добавления нового метода searchText в класс SuffixTree , используя шаблон для поиска в качестве входных данных:
public List<String> searchText(String pattern) {
// ...
}
Затем, чтобы проверить, существует ли шаблон в нашем дереве суффиксов, мы вызываем наш вспомогательный метод getAllNodesInTraversePath с установленным флагом только для точных совпадений, в отличие от добавления данных, когда мы разрешали частичные совпадения:
List<Node> nodes = getAllNodesInTraversePath(pattern, root, false);
Затем мы получаем список узлов, соответствующих нашему шаблону. Последний узел в списке указывает узел, до которого шаблон точно совпал. Итак, нашим следующим шагом будет получение всех конечных узлов, происходящих из этого последнего соответствующего узла, и получение позиций, хранящихся в этих конечных узлах.
Для этого создадим отдельный метод getPositions . Мы проверим, хранит ли данный узел последнюю часть суффикса, чтобы решить, нужно ли возвращать значение его позиции. И мы сделаем это рекурсивно для каждого дочернего элемента данного узла:
private List<Integer> getPositions(Node node) {
List<Integer> positions = new ArrayList<>();
if (node.getText().endsWith(WORD_TERMINATION)) {
positions.add(node.getPosition());
}
for (int i = 0; i < node.getChildren().size(); i++) {
positions.addAll(getPositions(node.getChildren().get(i)));
}
return positions;
}
Когда у нас есть набор позиций, следующим шагом будет использование его для обозначения шаблонов в тексте, который мы сохранили в нашем дереве суффиксов. Значение позиции указывает, где начинается суффикс, а длина шаблона указывает, сколько символов нужно сместить от начальной точки. Применяя эту логику, давайте создадим простой служебный метод:
private String markPatternInText(Integer startPosition, String pattern) {
String matchingTextLHS = fullText.substring(0, startPosition);
String matchingText = fullText.substring(startPosition, startPosition + pattern.length());
String matchingTextRHS = fullText.substring(startPosition + pattern.length());
return matchingTextLHS + "[" + matchingText + "]" + matchingTextRHS;
}
Теперь у нас есть готовые вспомогательные методы. Поэтому мы можем добавить их в наш метод поиска и завершить логику :
public List<String> searchText(String pattern) {
List<String> result = new ArrayList<>();
List<Node> nodes = getAllNodesInTraversePath(pattern, root, false);
if (nodes.size() > 0) {
Node lastNode = nodes.get(nodes.size() - 1);
if (lastNode != null) {
List<Integer> positions = getPositions(lastNode);
positions = positions.stream()
.sorted()
.collect(Collectors.toList());
positions.forEach(m -> result.add((markPatternInText(m, pattern))));
}
}
return result;
}
8. Тестирование
Теперь, когда у нас есть наш алгоритм, давайте проверим его.
Во-первых, давайте сохраним текст в нашем SuffixTree :
SuffixTree suffixTree = new SuffixTree("havanabanana");
Далее, давайте найдем допустимый шаблон a :
List<String> matches = suffixTree.searchText("a");
matches.stream().forEach(m -> LOGGER.debug(m));
Запуск кода дает нам шесть совпадений, как и ожидалось:
h[a]vanabanana
hav[a]nabanana
havan[a]banana
havanab[a]nana
havanaban[a]na
havanabanan[a]
Далее давайте найдем другой допустимый шаблон nab :
List<String> matches = suffixTree.searchText("nab");
matches.stream().forEach(m -> LOGGER.debug(m));
Запуск кода дает нам только одно совпадение, как и ожидалось:
hava[nab]anana
Наконец, давайте найдем неверный шаблон nag :
List<String> matches = suffixTree.searchText("nag");
matches.stream().forEach(m -> LOGGER.debug(m));
Запуск кода не дает нам никаких результатов. Мы видим, что совпадения должны быть точными, а не частичными.
Таким образом, наш алгоритм поиска паттернов смог удовлетворить все ожидания, которые мы изложили в начале этого урока.
9. Временная сложность
При построении суффиксного дерева для заданного текста длины t временная сложность составляет `` O (t) .
Тогда для поиска шаблона длины p временная сложность равна O(p) . Вспомните, что для поиска методом грубой силы это было O(p*t) . Таким образом, поиск шаблона становится быстрее после предварительной обработки текста .
10. Заключение
В этой статье мы впервые поняли концепции трех структур данных — trie, suffix trie и suffix tree. Затем мы увидели, как дерево суффиксов можно использовать для компактного хранения суффиксов.
Позже мы увидели, как использовать дерево суффиксов для хранения данных и выполнения поиска по шаблону.
Как всегда, исходный код с тестами доступен на GitHub .