1. Введение
В этом руководстве мы изучим процесс создания набора мощности заданного набора в Java.
Напомню, что для каждого набора размера n существует набор мощности размера 2 n . Мы узнаем, как получить его, используя различные методы.
2. Определение набора мощности
Набор мощности данного набора S — это набор всех подмножеств S , включая само S и пустое множество.
Например, для данного набора:
{"APPLE", "ORANGE", "MANGO"}
силовой набор такой:
{
{},
{"APPLE"},
{"ORANGE"},
{"APPLE", "ORANGE"},
{"MANGO"},
{"APPLE", "MANGO"},
{"ORANGE", "MANGO"},
{"APPLE", "ORANGE", "MANGO"}
}
Поскольку это также набор подмножеств, порядок его внутренних подмножеств не важен, и они могут появляться в любом порядке:
{
{},
{"MANGO"},
{"ORANGE"},
{"ORANGE", "MANGO"},
{"APPLE"},
{"APPLE", "MANGO"},
{"APPLE", "ORANGE"},
{"APPLE", "ORANGE", "MANGO"}
}
3. Библиотека гуавы
В библиотеке Google Guava есть несколько полезных утилит Set , например power set. Таким образом, мы можем легко использовать его и для получения набора мощностей данного набора:
@Test
public void givenSet_WhenGuavaLibraryGeneratePowerSet_ThenItContainsAllSubsets() {
ImmutableSet<String> set = ImmutableSet.of("APPLE", "ORANGE", "MANGO");
Set<Set<String>> powerSet = Sets.powerSet(set);
Assertions.assertEquals((1 << set.size()), powerSet.size());
MatcherAssert.assertThat(powerSet, Matchers.containsInAnyOrder(
ImmutableSet.of(),
ImmutableSet.of("APPLE"),
ImmutableSet.of("ORANGE"),
ImmutableSet.of("APPLE", "ORANGE"),
ImmutableSet.of("MANGO"),
ImmutableSet.of("APPLE", "MANGO"),
ImmutableSet.of("ORANGE", "MANGO"),
ImmutableSet.of("APPLE", "ORANGE", "MANGO")
));
}
Guava powerSet внутренне работает через интерфейс Iterator таким образом, что когда запрашивается следующее подмножество, подмножество вычисляется и возвращается. Таким образом, сложность пространства снижается до O(n) вместо O(2 n ) .
Но как Гуава достигает этого?
4. Подход к генерации набора мощности
4.1. Алгоритм
Давайте теперь обсудим возможные шаги для создания алгоритма этой операции.
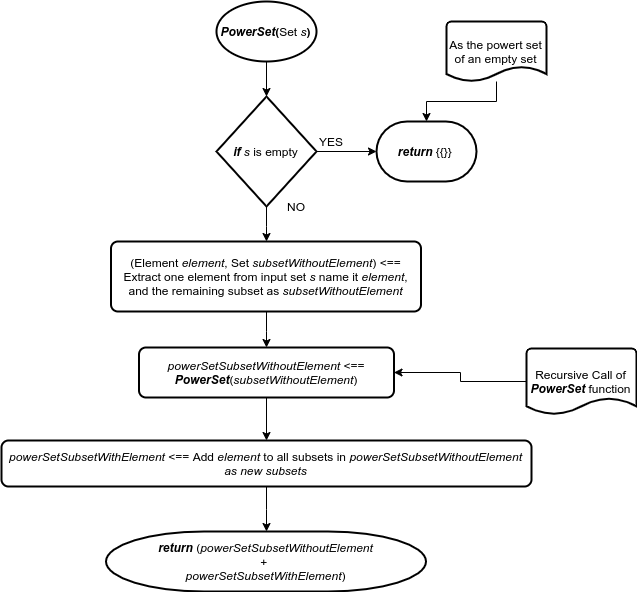
Степенной набор пустого набора равен {{}} , в котором он содержит только один пустой набор, так что это наш простейший случай.
Для каждого набора S , отличного от пустого, мы сначала извлекаем один элемент и называем его — element . Затем для остальных элементов набора subsetWithoutElement мы рекурсивно вычисляем их набор мощности — и называем его как-то вроде powerSet S ubsetWithoutElement . Затем, добавляя извлеченный элемент ко всем множествам в powerSet S ubsetWithoutElement , мы получаем powerSet S ubsetWithElement.
Теперь набор мощности S является объединением powerSetSubsetWithoutElement и powerSetSubsetWithElement :
[
](/lessons/b/-wp-content-uploads-2020-01-powerSet-Example-png)
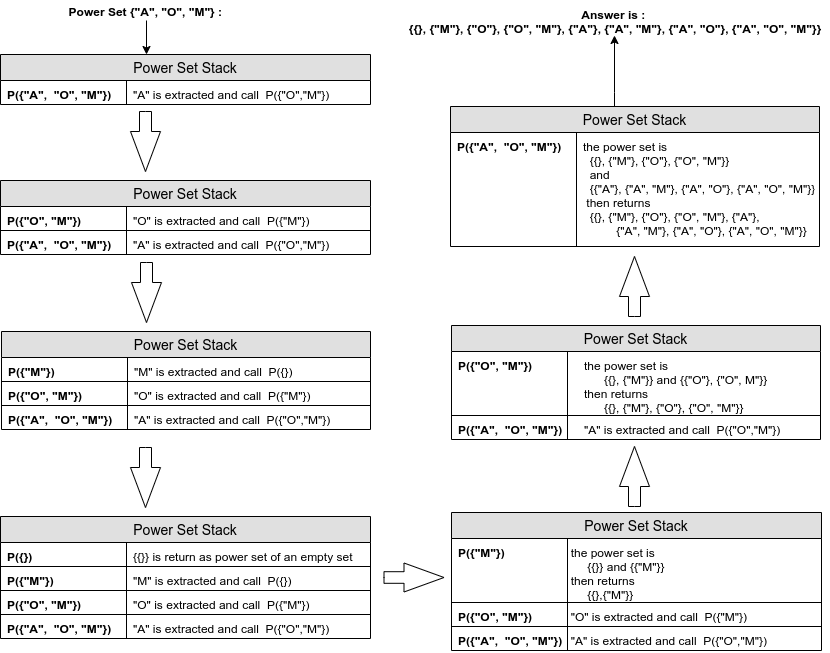
Давайте посмотрим на пример стека рекурсивного набора мощности для данного набора {"ЯБЛОКО", "АПЕЛЬСИН", "МАНГО"} .
Для улучшения читаемости изображения мы используем краткие формы имен: P означает функцию набора мощности, а «A», «O», «M» — краткие формы «ЯБЛОКО», «АПЕЛЬСИН» и «МАНГО» соответственно:
4.2. Реализация
Итак, для начала напишем Java-код для извлечения одного элемента и получения остальных подмножеств:
T element = set.iterator().next();
Set<T> subsetWithoutElement = new HashSet<>();
for (T s : set) {
if (!s.equals(element)) {
subsetWithoutElement.add(s);
}
}
Затем мы хотим получить набор функций subsetWithoutElement :
Set<Set<T>> powersetSubSetWithoutElement = recursivePowerSet(subsetWithoutElement);
Затем нам нужно добавить этот набор мощности обратно в оригинал:
Set<Set<T>> powersetSubSetWithElement = new HashSet<>();
for (Set<T> subsetWithoutElement : powerSetSubSetWithoutElement) {
Set<T> subsetWithElement = new HashSet<>(subsetWithoutElement);
subsetWithElement.add(element);
powerSetSubSetWithElement.add(subsetWithElement);
}
Наконец, объединение powerSetSubSetWithoutElement и powerSetSubSetWithElement представляет собой набор мощности данного входного набора:
Set<Set<T>> powerSet = new HashSet<>();
powerSet.addAll(powerSetSubSetWithoutElement);
powerSet.addAll(powerSetSubSetWithElement);
Если мы соединим все наши фрагменты кода вместе, мы увидим наш конечный продукт:
public Set<Set<T>> recursivePowerSet(Set<T> set) {
if (set.isEmpty()) {
Set<Set<T>> ret = new HashSet<>();
ret.add(set);
return ret;
}
T element = set.iterator().next();
Set<T> subSetWithoutElement = getSubSetWithoutElement(set, element);
Set<Set<T>> powerSetSubSetWithoutElement = recursivePowerSet(subSetWithoutElement);
Set<Set<T>> powerSetSubSetWithElement = addElementToAll(powerSetSubSetWithoutElement, element);
Set<Set<T>> powerSet = new HashSet<>();
powerSet.addAll(powerSetSubSetWithoutElement);
powerSet.addAll(powerSetSubSetWithElement);
return powerSet;
}
4.3. Примечания для модульных тестов
Теперь давайте тестировать. У нас есть несколько критериев для подтверждения:
- Во-первых, мы проверяем размер набора мощности, и он должен быть равен
2 nдля набора размераn. - Тогда каждый элемент будет встречаться только один раз в подмножестве и
2 n-1разных подмножествах. - Наконец, каждое подмножество должно появиться один раз.
Если все эти условия соблюдены, мы можем быть уверены, что наша функция работает. Теперь, когда мы использовали Set<Set> , мы уже знаем, что повторений нет. В этом случае нам нужно только проверить размер набора мощности и количество вхождений каждого элемента в подмножествах.
Чтобы проверить размер набора мощности, мы можем использовать:
MatcherAssert.assertThat(powerSet, IsCollectionWithSize.hasSize((1 << set.size())));
И проверить количество вхождений каждого элемента:
Map<String, Integer> counter = new HashMap<>();
for (Set<String> subset : powerSet) {
for (String name : subset) {
int num = counter.getOrDefault(name, 0);
counter.put(name, num + 1);
}
}
counter.forEach((k, v) -> Assertions.assertEquals((1 << (set.size() - 1)), v.intValue()));
Наконец, если мы можем собрать все вместе в один модульный тест:
@Test
public void givenSet_WhenPowerSetIsCalculated_ThenItContainsAllSubsets() {
Set<String> set = RandomSetOfStringGenerator.generateRandomSet();
Set<Set<String>> powerSet = new PowerSet<String>().recursivePowerSet(set);
MatcherAssert.assertThat(powerSet, IsCollectionWithSize.hasSize((1 << set.size())));
Map<String, Integer> counter = new HashMap<>();
for (Set<String> subset : powerSet) {
for (String name : subset) {
int num = counter.getOrDefault(name, 0);
counter.put(name, num + 1);
}
}
counter.forEach((k, v) -> Assertions.assertEquals((1 << (set.size() - 1)), v.intValue()));
}
5. Оптимизация
В этом разделе мы постараемся свести к минимуму пространство и уменьшить количество внутренних операций для оптимального вычисления набора мощностей.
5.1. Структура данных
Как мы видим в данном подходе нам нужно много вычитаний в рекурсивном вызове, который потребляет большое количество времени и памяти.
Вместо этого мы можем сопоставить каждое множество или подмножество некоторым другим понятиям, чтобы уменьшить количество операций.
Во-первых, нам нужно присвоить возрастающее число, начиная с 0, каждому объекту в заданном наборе S , что означает, что мы работаем с упорядоченным списком чисел.
Например, для заданного набора {"ЯБЛОКО", "АПЕЛЬСИН", "МАНГО"} получаем:
«ЯБЛОКО» -> 0
«ОРАНЖЕВЫЙ» -> 1
«МАНГО» -> 2
Итак, теперь вместо того, чтобы генерировать подмножества S , мы генерируем их для упорядоченного списка [0, 1, 2], и по мере его упорядочения мы можем моделировать вычитания по начальному индексу.
Например, если начальный индекс равен 1, это означает, что мы генерируем набор мощностей [1,2].
Чтобы получить сопоставленный идентификатор из объекта и наоборот, мы сохраняем обе стороны сопоставления. Используя наш пример, мы храним как («MANGO» -> 2) , так и (2 -> «MANGO») . Поскольку отображение чисел началось с нуля, поэтому для обратной карты мы можем использовать простой массив для извлечения соответствующего объекта.
Одной из возможных реализаций этой функции может быть:
private Map<T, Integer> map = new HashMap<>();
private List<T> reverseMap = new ArrayList<>();
private void initializeMap(Collection<T> collection) {
int mapId = 0;
for (T c : collection) {
map.put(c, mapId++);
reverseMap.add(c);
}
}
Теперь для представления подмножеств есть две известные идеи:
- Представление индекса
- Двоичное представление
5.2. Представление индекса
Каждое подмножество представлено индексом своих значений. Например, отображение индекса данного набора {"ЯБЛОКО", "АПЕЛЬСИН", "МАНГО"} будет таким:
{
{} -> {}
[0] -> {"APPLE"}
[1] -> {"ORANGE"}
[0,1] -> {"APPLE", "ORANGE"}
[2] -> {"MANGO"}
[0,2] -> {"APPLE", "MANGO"}
[1,2] -> {"ORANGE", "MANGO"}
[0,1,2] -> {"APPLE", "ORANGE", "MANGO"}
}
Итак, мы можем получить соответствующий набор из подмножества индексов с заданным отображением:
private Set<Set<T>> unMapIndex(Set<Set<Integer>> sets) {
Set<Set<T>> ret = new HashSet<>();
for (Set<Integer> s : sets) {
HashSet<T> subset = new HashSet<>();
for (Integer i : s) {
subset.add(reverseMap.get(i));
}
ret.add(subset);
}
return ret;
}
5.3. Двоичное представление
Или мы можем представить каждое подмножество с помощью двоичного кода. Если элемент фактического набора существует в этом подмножестве, его соответствующее значение равно 1 ; в противном случае это 0 .
Для нашего примера с фруктами набор мощности будет таким:
{
[0,0,0] -> {}
[1,0,0] -> {"APPLE"}
[0,1,0] -> {"ORANGE"}
[1,1,0] -> {"APPLE", "ORANGE"}
[0,0,1] -> {"MANGO"}
[1,0,1] -> {"APPLE", "MANGO"}
[0,1,1] -> {"ORANGE", "MANGO"}
[1,1,1] -> {"APPLE", "ORANGE", "MANGO"}
}
Итак, мы можем получить соответствующий набор из двоичного подмножества с заданным отображением:
private Set<Set<T>> unMapBinary(Collection<List<Boolean>> sets) {
Set<Set<T>> ret = new HashSet<>();
for (List<Boolean> s : sets) {
HashSet<T> subset = new HashSet<>();
for (int i = 0; i < s.size(); i++) {
if (s.get(i)) {
subset.add(reverseMap.get(i));
}
}
ret.add(subset);
}
return ret;
}
5.4. Рекурсивная реализация алгоритма
На этом шаге мы попробуем реализовать предыдущий код, используя обе структуры данных.
Перед вызовом одной из этих функций нам нужно вызвать метод initializeMap , чтобы получить упорядоченный список. Кроме того, после создания нашей структуры данных нам нужно вызвать соответствующую функцию unMap для извлечения фактических объектов:
public Set<Set<T>> recursivePowerSetIndexRepresentation(Collection<T> set) {
initializeMap(set);
Set<Set<Integer>> powerSetIndices = recursivePowerSetIndexRepresentation(0, set.size());
return unMapIndex(powerSetIndices);
}
Итак, давайте попробуем свои силы в представлении индекса:
private Set<Set<Integer>> recursivePowerSetIndexRepresentation(int idx, int n) {
if (idx == n) {
Set<Set<Integer>> empty = new HashSet<>();
empty.add(new HashSet<>());
return empty;
}
Set<Set<Integer>> powerSetSubset = recursivePowerSetIndexRepresentation(idx + 1, n);
Set<Set<Integer>> powerSet = new HashSet<>(powerSetSubset);
for (Set<Integer> s : powerSetSubset) {
HashSet<Integer> subSetIdxInclusive = new HashSet<>(s);
subSetIdxInclusive.add(idx);
powerSet.add(subSetIdxInclusive);
}
return powerSet;
}
Теперь давайте посмотрим на бинарный подход:
private Set<List<Boolean>> recursivePowerSetBinaryRepresentation(int idx, int n) {
if (idx == n) {
Set<List<Boolean>> powerSetOfEmptySet = new HashSet<>();
powerSetOfEmptySet.add(Arrays.asList(new Boolean[n]));
return powerSetOfEmptySet;
}
Set<List<Boolean>> powerSetSubset = recursivePowerSetBinaryRepresentation(idx + 1, n);
Set<List<Boolean>> powerSet = new HashSet<>();
for (List<Boolean> s : powerSetSubset) {
List<Boolean> subSetIdxExclusive = new ArrayList<>(s);
subSetIdxExclusive.set(idx, false);
powerSet.add(subSetIdxExclusive);
List<Boolean> subSetIdxInclusive = new ArrayList<>(s);
subSetIdxInclusive.set(idx, true);
powerSet.add(subSetIdxInclusive);
}
return powerSet;
}
5.5. Итерация через [0, 2 n )
Теперь есть хорошая оптимизация, которую мы можем сделать с двоичным представлением. Если мы посмотрим на это, мы увидим, что каждая строка эквивалентна двоичному формату числа в [0, 2 n ).
Итак, если мы перебираем числа от 0 до 2 n , мы можем преобразовать этот индекс в двоичный и использовать его для создания логического представления каждого подмножества:
private List<List<Boolean>> iterativePowerSetByLoopOverNumbers(int n) {
List<List<Boolean>> powerSet = new ArrayList<>();
for (int i = 0; i < (1 << n); i++) {
List<Boolean> subset = new ArrayList<>(n);
for (int j = 0; j < n; j++)
subset.add(((1 << j) & i) > 0);
powerSet.add(subset);
}
return powerSet;
}
5.6. Подмножества с минимальными изменениями по коду Грея
Теперь, если мы определим любую биективную функцию от двоичного представления длины n до числа в [0, 2 n ) , мы можем генерировать подмножества в любом порядке, который мы хотим.
Код Грея — это хорошо известная функция, которая используется для генерации двоичных представлений чисел таким образом, чтобы двоичное представление последовательных чисел отличалось только одним битом (даже разница между последним и первым числом равна единице).
Таким образом, мы можем оптимизировать это еще немного:
private List<List<Boolean>> iterativePowerSetByLoopOverNumbersWithGrayCodeOrder(int n) {
List<List<Boolean>> powerSet = new ArrayList<>();
for (int i = 0; i < (1 << n); i++) {
List<Boolean> subset = new ArrayList<>(n);
for (int j = 0; j < n; j++) {
int grayEquivalent = i ^ (i >> 1);
subset.add(((1 << j) & grayEquivalent) > 0);
}
powerSet.add(subset);
}
return powerSet;
}
6. Ленивая загрузка
Чтобы свести к минимуму использование пространства набора мощности, который составляет O(2 n ) , мы можем использовать интерфейс Iterator для ленивой выборки каждого подмножества, а также каждого элемента в каждом подмножестве.
6.1. ListIterator
Во-первых, чтобы иметь возможность перебирать от 0 до 2 n , у нас должен быть специальный итератор , который перебирает этот диапазон, но не использует весь диапазон заранее.
Чтобы решить эту проблему, мы будем использовать две переменные; один для размера, который равен 2 n , а другой для текущего индекса подмножества. Наша функция hasNext() проверит, что position меньше size :
abstract class ListIterator<K> implements Iterator<K> {
protected int position = 0;
private int size;
public ListIterator(int size) {
this.size = size;
}
@Override
public boolean hasNext() {
return position < size;
}
}
И наша функция next() возвращает подмножество для текущей позиции и увеличивает значение позиции на единицу:
@Override
public Set<E> next() {
return new Subset<>(map, reverseMap, position++);
}
6.2. Подмножество
Для ленивой загрузки Subset мы определяем класс, который расширяет AbstractSet , и переопределяем некоторые его функции.
Перебирая все биты, равные 1 , в принимающей маске (или позиции) Subset , мы можем реализовать Iterator и другие методы в AbstractSet .
Например, size() — это количество единиц в принимающей маске :
@Override
public int size() {
return Integer.bitCount(mask);
}
А функция contains() определяет, равен ли соответствующий бит в маске 1 или нет:
@Override
public boolean contains(@Nullable Object o) {
Integer index = map.get(o);
return index != null && (mask & (1 << index)) != 0;
}
Мы используем другую переменную — restSetBits — для ее изменения всякий раз, когда мы извлекаем соответствующий элемент в подмножестве, мы меняем этот бит на 0 . Затем функция hasNext() проверяет, не равен ли оставшийся набор битов нулю (то есть имеет ли он хотя бы один бит со значением 1 ):
@Override
public boolean hasNext() {
return remainingSetBits != 0;
}
А функция next() использует самую правую 1 из оставшегося набора битов, затем преобразует ее в 0 и также возвращает соответствующий элемент:
@Override
public E next() {
int index = Integer.numberOfTrailingZeros(remainingSetBits);
if (index == 32) {
throw new NoSuchElementException();
}
remainingSetBits &= ~(1 << index);
return reverseMap.get(index);
}
6.3. PowerSet
Чтобы иметь класс PowerSet с отложенной загрузкой , нам нужен класс, расширяющий AbstractSet<Set<T>>.
Функция size() просто равна 2 в степени размера набора:
@Override
public int size() {
return (1 << this.set.size());
}
Поскольку набор мощности будет содержать все возможные подмножества входного набора, функция contains(Object o) проверяет, существуют ли все элементы объекта o в reverseMap (или во входном наборе):
@Override
public boolean contains(@Nullable Object obj) {
if (obj instanceof Set) {
Set<?> set = (Set<?>) obj;
return reverseMap.containsAll(set);
}
return false;
}
Чтобы проверить равенство данного объекта с этим классом, мы можем только проверить , равен ли входной набор данному объекту :
@Override
public boolean equals(@Nullable Object obj) {
if (obj instanceof PowerSet) {
PowerSet<?> that = (PowerSet<?>) obj;
return set.equals(that.set);
}
return super.equals(obj);
}
Функция iterator() возвращает экземпляр ListIterator , который мы уже определили:
@Override
public Iterator<Set<E>> iterator() {
return new ListIterator<Set<E>>(this.size()) {
@Override
public Set<E> next() {
return new Subset<>(map, reverseMap, position++);
}
};
}
Библиотека Guava использует эту идею ленивой загрузки, и эти PowerSet и Subset являются эквивалентными реализациями библиотеки Guava.
Для получения дополнительной информации проверьте их исходный код и документацию .
Кроме того, если мы хотим выполнить параллельную операцию над подмножествами в PowerSet , мы можем вызывать Subset для разных значений в ThreadPool .
7. Резюме
Подводя итог, сначала мы изучили, что такое силовой набор. Затем мы сгенерировали его с помощью библиотеки Guava. После этого мы изучили подход и то, как его реализовать, а также как написать для него юнит-тест.
Наконец, мы использовали интерфейс Iterator для оптимизации пространства генерации подмножеств, а также их внутренних элементов.
Как всегда, исходный код доступен на GitHub .