1. Обзор
В этом уроке мы рассмотрим концепцию поиска соседей в двумерном пространстве . Затем мы рассмотрим его реализацию на Java.
2. Одномерный поиск против двумерного поиска
Мы знаем, что бинарный поиск — это эффективный алгоритм поиска точного совпадения в списке элементов с использованием подхода «разделяй и властвуй».
Давайте теперь рассмотрим двумерную область, где каждый элемент представлен координатами XY (точками) на плоскости .
Однако предположим, что вместо точного совпадения мы хотим найти соседей данной точки на плоскости. Понятно, что если нам нужны ближайшие n совпадений, то бинарный поиск не сработает . Это связано с тем, что бинарный поиск может сравнивать два элемента только по одной оси, тогда как нам нужно иметь возможность сравнивать их по двум осям.
В следующем разделе мы рассмотрим альтернативу структуре данных двоичного дерева.
3. Квадри
Дерево квадрантов — это пространственная древовидная структура данных, в которой каждый узел имеет ровно четыре дочерних элемента. Каждый дочерний элемент может быть либо точкой, либо списком, содержащим четыре поддерева квадрантов.
Точка хранит данные — например, координаты XY . Область представляет собой замкнутую границу, в пределах которой может быть сохранена точка. Он используется для определения области досягаемости дерева квадрантов.
Давайте лучше разберемся в этом на примере 10 координат в произвольном порядке:
(21,25), (55,53), (70,318), (98,302), (49,229), (135,229), (224,292), (206,321), (197,258), (245,238)
Первые три значения будут сохранены в виде точек под корневым узлом, как показано на крайнем левом рисунке.
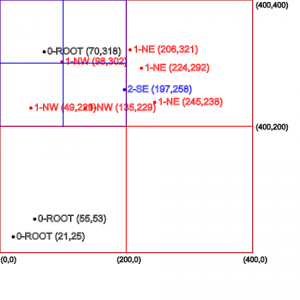
Корневой узел не может вместить новые точки, так как он достиг своей емкости в три точки. Поэтому разделим область корневого узла на четыре равных квадранта .
Каждый из этих квадрантов может хранить три точки и дополнительно содержать четыре квадранта в пределах своей границы. Это можно сделать рекурсивно, в результате чего получится дерево квадрантов, откуда структура данных дерева квадрантов и получила свое название.
На среднем рисунке выше мы можем видеть квадранты, созданные из корневого узла, и то, как следующие четыре точки хранятся в этих квадрантах.
Наконец, крайний правый рисунок показывает, как один квадрант снова подразделяется, чтобы разместить больше точек в этой области, в то время как другие квадранты все еще могут принимать новые точки.
Теперь мы посмотрим, как реализовать этот алгоритм на Java.
4. Структура данных
Давайте создадим структуру данных quadtree. Нам понадобятся три класса домена.
Во- первых, мы создадим класс Point для хранения координат XY :
public class Point {
private float x;
private float y;
public Point(float x, float y) {
this.x = x;
this.y = y;
}
// getters & toString()
}
Во-вторых, давайте создадим класс Region для определения границ квадранта :
public class Region {
private float x1;
private float y1;
private float x2;
private float y2;
public Region(float x1, float y1, float x2, float y2) {
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
}
// getters & toString()
}
Наконец, давайте создадим класс QuadTree для хранения данных в виде экземпляров Point и дочерних элементов в виде классов QuadTree :
public class QuadTree {
private static final int MAX_POINTS = 3;
private Region area;
private List<Point> points = new ArrayList<>();
private List<QuadTree> quadTrees = new ArrayList<>();
public QuadTree(Region area) {
this.area = area;
}
}
Чтобы создать экземпляр объекта QuadTree , мы указываем его площадь, используя класс Region через конструктор.
5. Алгоритм
Прежде чем мы напишем нашу основную логику для хранения данных, давайте добавим несколько вспомогательных методов. Они пригодятся позже.
5.1. Вспомогательные методы
Давайте изменим наш класс Region .
Во-первых, давайте создадим метод containsPoint , чтобы указать, попадает ли данная точка внутрь или за пределы области области :
public boolean containsPoint(Point point) {
return point.getX() >= this.x1
&& point.getX() < this.x2
&& point.getY() >= this.y1
&& point.getY() < this.y2;
}
Далее давайте создадим метод doOverlap , чтобы указать, перекрывается ли данная область с другой областью :
public boolean doesOverlap(Region testRegion) {
if (testRegion.getX2() < this.getX1()) {
return false;
}
if (testRegion.getX1() > this.getX2()) {
return false;
}
if (testRegion.getY1() > this.getY2()) {
return false;
}
if (testRegion.getY2() < this.getY1()) {
return false;
}
return true;
}
Наконец, давайте создадим метод getQuadrant для разделения диапазона на четыре равных квадранта и возврата указанного:
public Region getQuadrant(int quadrantIndex) {
float quadrantWidth = (this.x2 - this.x1) / 2;
float quadrantHeight = (this.y2 - this.y1) / 2;
// 0=SW, 1=NW, 2=NE, 3=SE
switch (quadrantIndex) {
case 0:
return new Region(x1, y1, x1 + quadrantWidth, y1 + quadrantHeight);
case 1:
return new Region(x1, y1 + quadrantHeight, x1 + quadrantWidth, y2);
case 2:
return new Region(x1 + quadrantWidth, y1 + quadrantHeight, x2, y2);
case 3:
return new Region(x1 + quadrantWidth, y1, x2, y1 + quadrantHeight);
}
return null;
}
5.2. Хранение данных
Теперь мы можем написать нашу логику для хранения данных. Начнем с определения нового метода addPoint в классе QuadTree для добавления новой точки. Этот метод вернет true , если точка была успешно добавлена:
public boolean addPoint(Point point) {
// ...
}
Далее, давайте напишем логику для обработки точки. Во-первых, нам нужно проверить, содержится ли точка в границах экземпляра QuadTree . Нам также необходимо убедиться, что экземпляр QuadTree не достиг максимального количества баллов MAX_POINTS .
Если оба условия выполнены, мы можем добавить новую точку:
if (this.area.containsPoint(point)) {
if (this.points.size() < MAX_POINTS) {
this.points.add(point);
return true;
}
}
С другой стороны, если мы достигли значения MAX_POINTS , нам нужно добавить новую точку в один из подквадрантов . Для этого мы проходим по дочернему списку quadTrees и вызываем тот же метод addPoint , который вернет истинное значение при успешном добавлении. Затем мы немедленно выходим из цикла, так как точка должна быть добавлена ровно в один квадрант .
Мы можем инкапсулировать всю эту логику внутри вспомогательного метода:
private boolean addPointToOneQuadrant(Point point) {
boolean isPointAdded;
for (int i = 0; i < 4; i++) {
isPointAdded = this.quadTrees.get(i)
.addPoint(point);
if (isPointAdded)
return true;
}
return false;
}
Кроме того, давайте создадим удобный метод createQuadrants для разделения текущего дерева квадрантов на четыре квадранта:
private void createQuadrants() {
Region region;
for (int i = 0; i < 4; i++) {
region = this.area.getQuadrant(i);
quadTrees.add(new QuadTree(region));
}
}
Мы будем вызывать этот метод для создания квадрантов только в том случае, если мы больше не можем добавлять новые точки . Это гарантирует, что наша структура данных использует оптимальное пространство памяти.
Собрав все вместе, мы получили обновленный метод addPoint :
public boolean addPoint(Point point) {
if (this.area.containsPoint(point)) {
if (this.points.size() < MAX_POINTS) {
this.points.add(point);
return true;
} else {
if (this.quadTrees.size() == 0) {
createQuadrants();
}
return addPointToOneQuadrant(point);
}
}
return false;
}
5.3. Поиск данных
Определив нашу структуру дерева квадрантов для хранения данных, мы теперь можем подумать о логике выполнения поиска.
Поскольку мы ищем соседние элементы, мы можем указать searchRegion в качестве отправной точки . Затем мы проверяем, не пересекается ли он с корневым регионом. Если это так, то мы добавляем все его дочерние точки, которые попадают в область поиска .
После корневой области мы попадаем в каждый из квадрантов и повторяем процесс. Так продолжается до тех пор, пока мы не достигнем конца дерева.
Напишем приведенную выше логику в виде рекурсивного метода в классе QuadTree :
public List<Point> search(Region searchRegion, List<Point> matches) {
if (matches == null) {
matches = new ArrayList<Point>();
}
if (!this.area.doesOverlap(searchRegion)) {
return matches;
} else {
for (Point point : points) {
if (searchRegion.containsPoint(point)) {
matches.add(point);
}
}
if (this.quadTrees.size() > 0) {
for (int i = 0; i < 4; i++) {
quadTrees.get(i)
.search(searchRegion, matches);
}
}
}
return matches;
}
6. Тестирование
Теперь, когда у нас есть наш алгоритм, давайте проверим его.
6.1. Заполнение данных
Во-первых, давайте заполним дерево квадрантов теми же 10 координатами, которые мы использовали ранее:
Region area = new Region(0, 0, 400, 400);
QuadTree quadTree = new QuadTree(area);
float[][] points = new float[][] { { 21, 25 }, { 55, 53 }, { 70, 318 }, { 98, 302 },
{ 49, 229 }, { 135, 229 }, { 224, 292 }, { 206, 321 }, { 197, 258 }, { 245, 238 } };
for (int i = 0; i < points.length; i++) {
Point point = new Point(points[i][0], points[i][1]);
quadTree.addPoint(point);
}
6.2. Поиск диапазона
Далее выполним поиск диапазона в области, ограниченной координатой нижней границы (200, 200) и координатой верхней границы (250, 250):
Region searchArea = new Region(200, 200, 250, 250);
List<Point> result = quadTree.search(searchArea, null);
Запуск кода даст нам одну ближайшую координату, содержащуюся в области поиска:
[[245.0 , 238.0]]
Попробуем другую область поиска между координатами (0, 0) и (100, 100):
Region searchArea = new Region(0, 0, 100, 100);
List<Point> result = quadTree.search(searchArea, null);
Запуск кода даст нам две ближайшие координаты для указанной области поиска:
[[21.0 , 25.0], [55.0 , 53.0]]
Заметим, что в зависимости от размера области поиска мы получаем ноль, одну или много точек. Итак, если нам дали точку и попросили найти n ближайших соседей, мы могли бы определить подходящую область поиска, в которой данная точка находится в центре .
Затем по всем полученным точкам операции поиска мы можем вычислить евклидовы расстояния между заданными точками и отсортировать их для получения ближайших соседей .
7. Временная сложность
Временная сложность запроса диапазона просто O(n) . Причина в том, что в худшем случае он должен пройти через каждый элемент, если указанная область поиска равна или больше, чем населенная область.
8. Заключение
В этой статье мы впервые поняли концепцию дерева квадрантов, сравнив его с бинарным деревом. Затем мы увидели, как его можно эффективно использовать для хранения данных, разбросанных по двумерному пространству.
Затем мы увидели, как хранить данные и выполнять поиск по диапазону.
Как всегда, исходный код с тестами доступен на GitHub .