1. Введение
В этом руководстве мы опишем алгоритм сортировки Shell в Java.
2. Обзор сортировки Шелла
2.1. Описание
Давайте сначала опишем алгоритм сортировки Шелла, чтобы мы знали, что мы пытаемся реализовать.
Сортировка Шелла основана на алгоритме сортировки вставками и относится к группе очень эффективных алгоритмов. Как правило, алгоритм разбивает исходный набор на более мелкие подмножества, а затем каждое из них сортируется с помощью сортировки вставками .
Но то, как он создает подмножества, не является простым. Он не выбирает соседние элементы для формирования подмножества, как можно было бы ожидать. Скорее, сортировка оболочки использует так называемый интервал или промежуток для создания подмножества. Например, если у нас есть разрыв I , это означает, что одно подмножество будет содержать элементы , которые находятся на расстоянии I позиции.
Во-первых, алгоритм сортирует элементы, находящиеся далеко друг от друга. Затем зазор становится меньше, и сравниваются более близкие элементы. Таким образом, некоторые элементы, которые не находятся в правильном положении, могут быть расположены быстрее, чем если бы мы создали подмножества из соседних элементов.
2.2. Пример
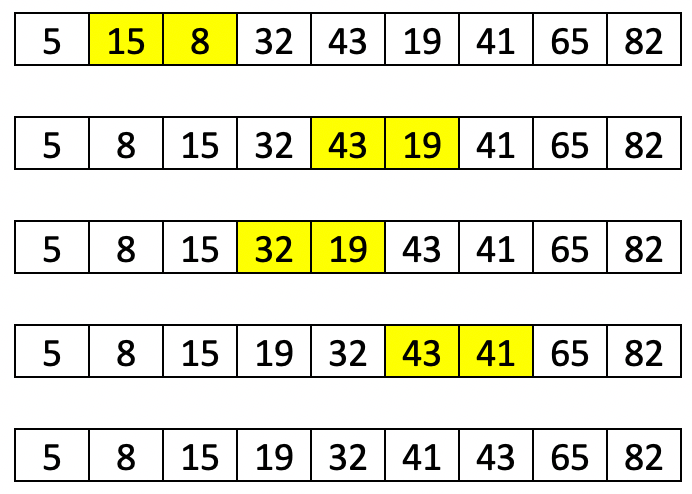
Давайте посмотрим это на примере с промежутками 3 и 1 и несортированным списком из 9 элементов:
Если мы будем следовать приведенному выше описанию, на первой итерации у нас будет три подмножества с 3 элементами (выделены одним цветом):
После сортировки каждого из подмножеств на первой итерации список будет выглядеть так:
Мы можем заметить, что, хотя у нас еще нет отсортированного списка, элементы теперь ближе к желаемым позициям.
Наконец, нам нужно сделать еще одну сортировку с приращением на единицу, и это на самом деле базовая сортировка вставками. Количество операций сдвига, которые нам нужно выполнить для сортировки списка, теперь меньше, чем было бы, если бы мы не делали первую итерацию:
2.3. Выбор последовательности гэпов
Как мы уже упоминали, сортировка оболочки имеет уникальный способ выбора последовательностей пробелов. Это трудная задача, и мы должны быть осторожны, чтобы не выбрать слишком мало или слишком много пробелов. Более подробную информацию можно найти в списке наиболее часто предлагаемых последовательностей гэпов .
3. Реализация
Давайте теперь посмотрим на реализацию. Мы будем использовать исходную последовательность Shell для увеличения интервала:
N/2, N/4, …, 1 (continuously dividing by 2)
Сама реализация не слишком сложна:
public void sort(int arrayToSort[]) {
int n = arrayToSort.length;
for (int gap = n / 2; gap > 0; gap /= 2) {
for (int i = gap; i < n; i++) {
int key = arrayToSort[i];
int j = i;
while (j >= gap && arrayToSort[j - gap] > key) {
arrayToSort[j] = arrayToSort[j - gap];
j -= gap;
}
arrayToSort[j] = key;
}
}
}
Сначала мы создали последовательность пробелов с помощью цикла for, а затем выполнили сортировку вставками для каждого размера пробела.
Теперь мы можем легко протестировать наш метод:
@Test
public void givenUnsortedArray_whenShellSort_thenSortedAsc() {
int[] input = {41, 15, 82, 5, 65, 19, 32, 43, 8};
ShellSort.sort(input);
int[] expected = {5, 8, 15, 19, 32, 41, 43, 65, 82};
assertArrayEquals("the two arrays are not equal", expected, input);
}
4. Сложность
Как правило, алгоритм сортировки Шелла очень эффективен для списков среднего размера . Сложность определить сложно, так как она во многом зависит от последовательности пропусков, но временная сложность варьируется от O(N) до O(N^2) .
Сложность пространства в наихудшем случае составляет O (N) с вспомогательным пространством O (1) .
5. Вывод
В этом руководстве мы описали сортировку Shell и проиллюстрировали, как мы можем реализовать ее в Java.
Как обычно, весь код можно найти на GitHub .