1. Введение
В этой статье мы рассмотрим возможные способы навигации по лабиринту с помощью Java.
Считайте лабиринт черно-белым изображением, где черные пиксели представляют собой стены, а белые пиксели представляют путь. Два белых пикселя являются особыми, один — это вход в лабиринт, а другой — выход.
Учитывая такой лабиринт, мы хотим найти путь от входа к выходу.
2. Моделирование лабиринта
Мы будем рассматривать лабиринт как двумерный целочисленный массив. Значение числовых значений в массиве будет соответствовать следующему соглашению:
- 0 -> Дорога
- 1 -> Стена
- 2 -> вход в лабиринт
- 3 -> Выход из лабиринта
- 4 -> Ячейка части пути от входа до выхода
Мы смоделируем лабиринт в виде графа . Вход и выход — это два специальных узла, между которыми необходимо определить путь.
Типичный граф имеет два свойства: узлы и ребра. Ребро определяет связность графа и связывает один узел с другим.
Следовательно, мы предполагаем четыре неявных ребра из каждого узла, связывающих данный узел с его левым, правым, верхним и нижним узлами.
Определим сигнатуру метода:
public List<Coordinate> solve(Maze maze) {
}
Входными данными для метода является лабиринт, содержащий двумерный массив с определенным выше соглашением об именах.
Ответом метода является список узлов, который формирует путь от узла входа к узлу выхода.
3. Рекурсивный возврат (DFS)
3.1. Алгоритм
Один довольно очевидный подход состоит в том, чтобы исследовать все возможные пути, которые в конечном итоге найдут путь, если он существует. Но такой подход будет иметь экспоненциальную сложность и не будет хорошо масштабироваться.
Тем не менее, можно настроить упомянутое выше решение грубой силы, отслеживая и отмечая посещенные узлы, чтобы получить путь за разумное время. Этот алгоритм также известен как поиск в глубину.
Этот алгоритм можно описать так:
- Если мы у стены или уже посещенного узла, вернуть отказ
- В противном случае, если мы являемся выходным узлом, верните успех
- В противном случае добавьте узел в список путей и рекурсивно перемещайтесь во всех четырех направлениях. Если возвращается ошибка, удалите узел из пути и верните ошибку. Список путей будет содержать уникальный путь, когда выход будет найден
Применим этот алгоритм к лабиринту, показанному на рис. 1(а), где S — начальная точка, а E — выход.
Для каждого узла мы проходим в каждом направлении по порядку: вправо, вниз, влево, вверх.
В 1(b) мы исследуем путь и врезаемся в стену. Затем мы возвращаемся назад до тех пор, пока не будет найден узел, у которого есть соседи, отличные от стены, и исследуем другой путь, как показано в 1(c).
Мы снова ударяемся о стену и повторяем процесс, чтобы наконец найти выход, как показано на 1(d):
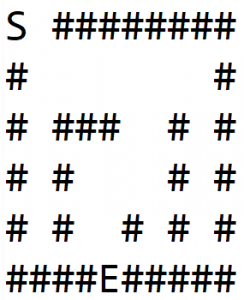
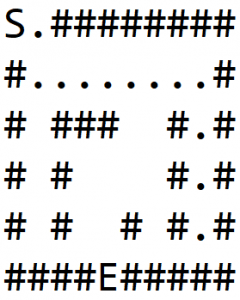


3.2. Реализация
Давайте теперь посмотрим на реализацию Java:
Во-первых, нам нужно определить четыре направления. Мы можем определить это в терминах координат. Эти координаты при добавлении к любой заданной координате вернут одну из соседних координат:
private static int[][] DIRECTIONS
= { { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 } };
Нам также нужен служебный метод, который добавит две координаты:
private Coordinate getNextCoordinate(
int row, int col, int i, int j) {
return new Coordinate(row + i, col + j);
}
Теперь мы можем определить сигнатуру методаsolve. Логика здесь простая — если есть путь от входа к выходу, то вернуть путь, иначе вернуть пустой список:
public List<Coordinate> solve(Maze maze) {
List<Coordinate> path = new ArrayList<>();
if (
explore(
maze,
maze.getEntry().getX(),
maze.getEntry().getY(),
path
)
) {
return path;
}
return Collections.emptyList();
}
Давайте определим метод исследования , упомянутый выше. Если есть путь, верните true со списком координат в аргументе path . Этот метод состоит из трех основных блоков.
Во-первых, мы отбрасываем недопустимые узлы, т. е. узлы, находящиеся за пределами лабиринта или являющиеся частью стены. После этого мы помечаем текущий узел как посещенный, чтобы не посещать один и тот же узел снова и снова.
Наконец, мы рекурсивно движемся во всех направлениях, если выход не найден:
private boolean explore(
Maze maze, int row, int col, List<Coordinate> path) {
if (
!maze.isValidLocation(row, col)
|| maze.isWall(row, col)
|| maze.isExplored(row, col)
) {
return false;
}
path.add(new Coordinate(row, col));
maze.setVisited(row, col, true);
if (maze.isExit(row, col)) {
return true;
}
for (int[] direction : DIRECTIONS) {
Coordinate coordinate = getNextCoordinate(
row, col, direction[0], direction[1]);
if (
explore(
maze,
coordinate.getX(),
coordinate.getY(),
path
)
) {
return true;
}
}
path.remove(path.size() - 1);
return false;
}
Это решение использует размер стека до размера лабиринта.
4. Вариант – кратчайший путь (BFS)
4.1. Алгоритм
Описанный выше рекурсивный алгоритм находит путь, но это не обязательно кратчайший путь. Чтобы найти кратчайший путь, мы можем использовать другой подход обхода графа, известный как поиск в ширину .
В DFS сначала исследовались один дочерний элемент и все его внуки, а затем переходили к другому дочернему элементу. В то время как в BFS мы исследуем всех непосредственных потомков, прежде чем переходить к внукам. Это гарантирует, что все узлы на определенном расстоянии от родительского узла будут исследованы одновременно.
Алгоритм можно изложить следующим образом:
Добавить начальный узел в очередь
Пока очередь не пуста, извлеките узел, сделайте следующее:
Если мы достигаем стены или узел уже посещен, переходим к следующей итерации.
Если выходной узел достигнут, вернуться от текущего узла к начальному узлу, чтобы найти кратчайший путь
В противном случае добавьте в очередь всех непосредственных соседей в четырех направлениях.
Здесь важно то, что узлы должны отслеживать своего родителя, т. е. откуда они были добавлены в очередь. Это важно, чтобы найти путь, когда встретится выходной узел.
Следующая анимация показывает все этапы исследования лабиринта с использованием этого алгоритма. Мы можем заметить, что все узлы на одинаковом расстоянии сначала исследуются, прежде чем перейти на следующий уровень:
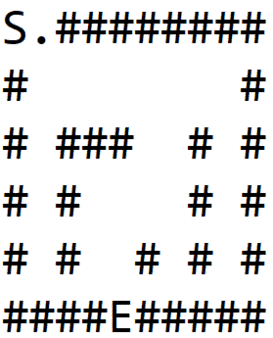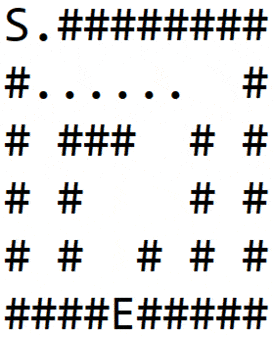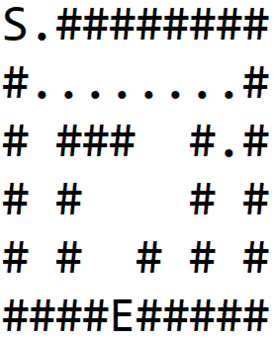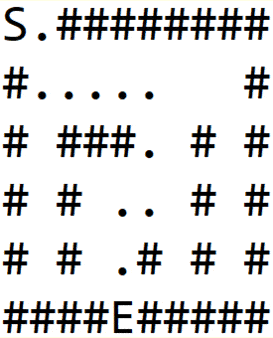
4.2. Реализация
Давайте теперь реализуем этот алгоритм на Java. Мы будем повторно использовать переменную DIRECTIONS , определенную в предыдущем разделе.
Давайте сначала определим служебный метод для возврата от заданного узла к его корню. Это будет использоваться для отслеживания пути после того, как выход будет найден:
private List<Coordinate> backtrackPath(
Coordinate cur) {
List<Coordinate> path = new ArrayList<>();
Coordinate iter = cur;
while (iter != null) {
path.add(iter);
iter = iter.parent;
}
return path;
}
Давайте теперь определим основной метод решения. Мы повторно используем три блока, используемых в реализации DFS, т. е. проверка узла, отметка посещенного узла и обход соседних узлов.
Мы просто сделаем одну небольшую модификацию. Вместо рекурсивного обхода мы будем использовать структуру данных FIFO для отслеживания соседей и их перебора:
public List<Coordinate> solve(Maze maze) {
LinkedList<Coordinate> nextToVisit
= new LinkedList<>();
Coordinate start = maze.getEntry();
nextToVisit.add(start);
while (!nextToVisit.isEmpty()) {
Coordinate cur = nextToVisit.remove();
if (!maze.isValidLocation(cur.getX(), cur.getY())
|| maze.isExplored(cur.getX(), cur.getY())
) {
continue;
}
if (maze.isWall(cur.getX(), cur.getY())) {
maze.setVisited(cur.getX(), cur.getY(), true);
continue;
}
if (maze.isExit(cur.getX(), cur.getY())) {
return backtrackPath(cur);
}
for (int[] direction : DIRECTIONS) {
Coordinate coordinate
= new Coordinate(
cur.getX() + direction[0],
cur.getY() + direction[1],
cur
);
nextToVisit.add(coordinate);
maze.setVisited(cur.getX(), cur.getY(), true);
}
}
return Collections.emptyList();
}
5. Вывод
В этом руководстве мы описали два основных алгоритма графа: поиск в глубину и поиск в ширину для решения лабиринта. Мы также коснулись того, как BFS определяет кратчайший путь от входа до выхода.
Для дальнейшего чтения поищите другие методы решения лабиринта, такие как A* и алгоритм Дейкстры.
Как всегда, полный код можно найти на GitHub .