Разделение и сортировка массивов с множеством повторяющихся записей с примерами Java

1. Обзор

Сложность алгоритмов во время выполнения часто зависит от характера входных данных.

В этом уроке мы увидим, как тривиальная реализация алгоритма быстрой сортировки имеет низкую производительность для повторяющихся элементов .

Далее мы изучим несколько вариантов быстрой сортировки для эффективного разделения и сортировки входных данных с высокой плотностью повторяющихся ключей.

2. Тривиальная быстрая сортировка

Quicksort — это эффективный алгоритм сортировки, основанный на парадигме «разделяй и властвуй». С функциональной точки зрения он работает с входным массивом на месте и переставляет элементы с помощью простых операций сравнения и замены .

2.1. Одноосевое разбиение

Тривиальная реализация алгоритма быстрой сортировки в значительной степени зависит от процедуры разбиения с одной точкой опоры. Другими словами, разбиение делит массив A=[ ap, ap+ 1 , ap +2 , … , ar ] на две части A[p..q] и A[q+1..r], такие что:

• Все элементы в первом разделе A[p..q] меньше или равны опорному значению A[q]
• Все элементы во втором разделе A[q+1..r] больше или равны опорному значению A[q]

После этого два раздела обрабатываются как независимые входные массивы и передаются алгоритму быстрой сортировки. Давайте посмотрим на быструю сортировку Ломуто в действии:

2.2. Производительность с повторяющимися элементами

Допустим, у нас есть массив A = [4, 4, 4, 4, 4, 4, 4], в котором все элементы равны.

При разбиении этого массива по одноосевой схеме мы получим два раздела. Первый раздел будет пустым, а второй раздел будет содержать N-1 элементов. Кроме того, каждый последующий вызов процедуры разделения будет уменьшать размер входных данных только на один . Давайте посмотрим, как это работает:

Поскольку процедура разбиения имеет линейную временную сложность, общая временная сложность в этом случае является квадратичной. Это наихудший сценарий для нашего входного массива.

3. Трехстороннее разделение

Чтобы эффективно отсортировать массив с большим количеством повторяющихся ключей, мы можем более ответственно относиться к одинаковым ключам. Идея состоит в том, чтобы поместить их в правильное положение, когда мы впервые встретимся с ними. Итак, мы ищем состояние трех разделов массива:

• Крайний левый раздел содержит элементы, которые строго меньше ключа раздела.
• ** Средний раздел содержит все элементы, равные ключу раздела ** . ****
• Крайний правый раздел содержит все элементы, которые строго больше ключа раздела.

Теперь мы углубимся в пару подходов, которые мы можем использовать для достижения трехстороннего разделения.

4. Подход Дейкстры

Подход Дейкстры — это эффективный способ трехстороннего разделения. Чтобы понять это, давайте рассмотрим классическую задачу программирования.

4.1. Проблема национального флага Нидерландов

Вдохновленный трехцветным флагом Нидерландов , Эдсгер Дейкстра предложил задачу программирования под названием « Задача национального флага Нидерландов» (DNF).

В двух словах, это задача на перестановку, когда нам даны шары трех цветов, расположенные случайным образом в ряд, и нас просят сгруппировать шары одного цвета вместе . Кроме того, перестановка должна гарантировать, что группы следуют правильному порядку.

Интересно, что проблема ДНФ проводит поразительную аналогию с трехсторонним разбиением массива с повторяющимися элементами.

Мы можем разделить все числа массива на три группы по заданному ключу:

• В красную группу входят все элементы, строго меньшие ключа
• В группу White входят все элементы, равные ключу
• Группа Blue содержит все элементы, которые строго больше ключа

4.2. Алгоритм

Один из подходов к решению проблемы ДНФ состоит в том, чтобы выбрать первый элемент в качестве ключа разбиения и просмотреть массив слева направо. Когда мы проверяем каждый элемент, мы перемещаем его в правильную группу, а именно «Меньше», «Равно» и «Больше».

Чтобы отслеживать процесс разбиения, нам понадобится помощь трех указателей, а именно lt , current и gt. В любой момент времени элементы слева от lt будут строго меньше ключа разбиения, а элементы справа от gt будут строго больше ключа .

Далее мы будем использовать текущий указатель для сканирования, а это значит, что все элементы, лежащие между текущим указателем и указателем gt , еще предстоит исследовать:

Для начала мы можем установить указатели lt и current в самом начале массива, а указатель gt в самом его конце:

Для каждого элемента, прочитанного через текущий указатель, мы сравниваем его с ключом разделения и выполняем одно из трех составных действий:

• Если input[current] < key , то мы меняем input[current] и input[lt] и увеличиваем оба указателя — current и lt .
• Если input[current] == key , то мы увеличиваем текущий указатель
• Если input[current] > key , то мы меняем input[current] и input[gt] и уменьшаем gt

В конце концов, мы остановимся, когда указатели current и gt пересекутся . При этом размер неисследованной области уменьшается до нуля, и у нас остается всего три необходимых раздела.

Наконец, давайте посмотрим, как этот алгоритм работает с входным массивом, содержащим повторяющиеся элементы:

4.3. Реализация

Во-первых, давайте напишем служебную процедуру с именем compare() для трехстороннего сравнения двух чисел:

public static int compare(int num1, int num2) {
    if (num1 > num2)
        return 1;
    else if (num1 < num2)
        return -1;
    else
        return 0;
}

Далее добавим метод swap() для обмена элементами по двум индексам одного и того же массива:

public static void swap(int[] array, int position1, int position2) {
    if (position1 != position2) {
        int temp = array[position1];
        array[position1] = array[position2];
        array[position2] = temp;
    }
}

Чтобы однозначно идентифицировать раздел в массиве, нам понадобятся его левый и правый граничные индексы. Итак, давайте продолжим и создадим класс Partition :

public class Partition {
    private int left;
    private int right;
}

Теперь мы готовы написать нашу трехэтапную процедуру partition() :

public static Partition partition(int[] input, int begin, int end) {
    int lt = begin, current = begin, gt = end;
    int partitioningValue = input[begin];

    while (current <= gt) {
        int compareCurrent = compare(input[current], partitioningValue);
        switch (compareCurrent) {
            case -1:
                swap(input, current++, lt++);
                break;
            case 0:
                current++;
                break;
            case 1:
                swap(input, current, gt--);
                break;
        }
    }
    return new Partition(lt, gt);
}

Наконец, давайте напишем метод quicksort() , который использует нашу трехстороннюю схему разбиения для рекурсивной сортировки левого и правого разделов :

public static void quicksort(int[] input, int begin, int end) {
    if (end <= begin)
        return;

    Partition middlePartition = partition(input, begin, end);

    quicksort(input, begin, middlePartition.getLeft() - 1);
    quicksort(input, middlePartition.getRight() + 1, end);
}

5. Подход Бентли-Макилроя

Джон Бентли и Дуглас Макилрой написали в соавторстве оптимизированную версию алгоритма Quicksort . Давайте разберемся и реализуем этот вариант на Java:

5.1. Схема разбиения

Суть алгоритма заключается в итерационной схеме разбиения. Поначалу весь массив чисел для нас неизведанная территория:

Затем мы начинаем исследовать элементы массива слева и справа. Всякий раз, когда мы входим или выходим из цикла исследования, мы можем визуализировать массив как состав пяти областей :

• На двух крайних концах лежат области, элементы которых равны значению разбиения
• Неисследованная область остается в центре, и ее размер продолжает уменьшаться с каждой итерацией.
• Слева от неисследованной области лежат все элементы меньше значения разбиения
• В правой части неисследованной области находятся элементы, превышающие значение разбиения.

В конце концов, наш цикл исследования заканчивается, когда больше нет элементов для исследования. На данном этапе размер неисследованной области фактически равен нулю , и у нас осталось только четыре области:

Затем мы перемещаем все элементы из двух равных областей в центре так, чтобы в центре была только одна равная область, окруженная меньшей областью слева и большей областью справа. Для этого сначала мы меняем местами элементы в левой равной области с элементами в правом конце меньшей области. Точно так же элементы в правой равной области меняются местами с элементами в левом конце большей области.

Наконец, у нас останется только три раздела , и мы можем далее использовать тот же подход для разделения меньшего и большего регионов.

5.2. Реализация

В нашей рекурсивной реализации трехфакторной быстрой сортировки нам потребуется вызвать нашу процедуру разделения для подмассивов, которые будут иметь другой набор нижних и верхних границ. Итак, наш метод partition() должен принимать три входа, а именно массив вместе с его левой и правой границами.

public static Partition partition(int input[], int begin, int end){
    // returns partition window
}

Для простоты мы можем выбрать значение разбиения как последний элемент массива . Кроме того, давайте определим две переменные left=begin и right=end для изучения массива внутрь.

Кроме того, нам также нужно отслеживать количество одинаковых элементов, лежащих в крайнем левом и крайнем правом углу . Итак, давайте инициализируем leftEqualKeysCount=0 и rightEqualKeysCount=0 , и теперь мы готовы исследовать и разбивать массив.

Сначала начинаем двигаться с обоих направлений и находим инверсию , при которой элемент слева не меньше значения разбиения, а элемент справа не больше значения разбиения. Затем, если два указателя слева и справа не пересеклись, мы меняем местами два элемента.

На каждой итерации мы перемещаем элементы, равные partitioningValue , к двум концам и увеличиваем соответствующий счетчик:

while (true) {
    while (input[left] < partitioningValue) left++; 
    
    while (input[right] > partitioningValue) {
        if (right == begin)
            break;
        right--;
    }

    if (left == right && input[left] == partitioningValue) {
        swap(input, begin + leftEqualKeysCount, left);
        leftEqualKeysCount++;
        left++;
    }

    if (left >= right) {
        break;
    }

    swap(input, left, right);

    if (input[left] == partitioningValue) {
        swap(input, begin + leftEqualKeysCount, left);
        leftEqualKeysCount++;
    }

    if (input[right] == partitioningValue) {
        swap(input, right, end - rightEqualKeysCount);
        rightEqualKeysCount++;
    }
    left++; right--;
}

На следующем этапе нам нужно переместить все равные элементы с двух концов в центр . После выхода из цикла левый указатель будет находиться на элементе, значение которого не меньше, чем partitioningValue . Используя этот факт, мы начинаем перемещать равные элементы с двух концов к центру:

right = left - 1;
for (int k = begin; k < begin + leftEqualKeysCount; k++, right--) { 
    if (right >= begin + leftEqualKeysCount)
        swap(input, k, right);
}
for (int k = end; k > end - rightEqualKeysCount; k--, left++) {
    if (left <= end - rightEqualKeysCount)
        swap(input, left, k);
}

На последнем этапе мы можем вернуть границы среднего раздела:

return new Partition(right + 1, left - 1);

Наконец, давайте посмотрим на демонстрацию нашей реализации на примере входных данных.

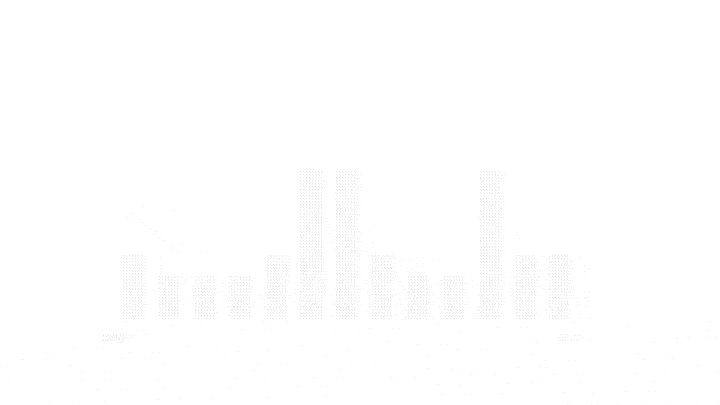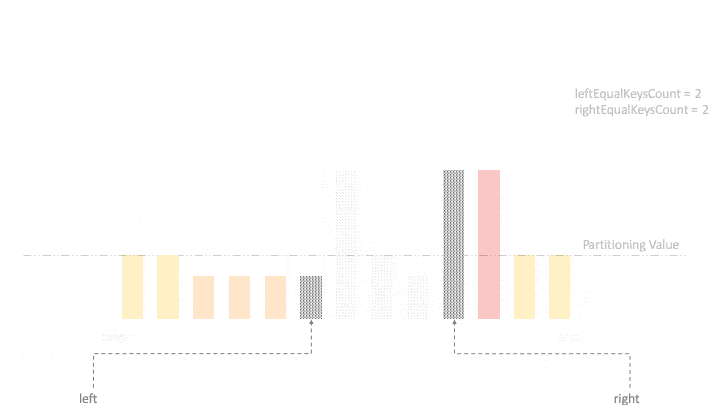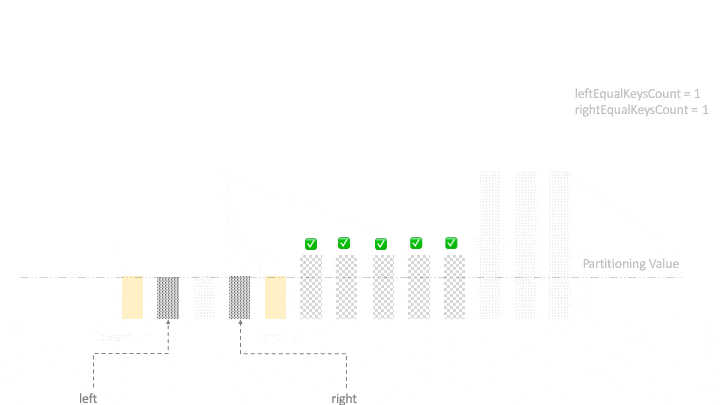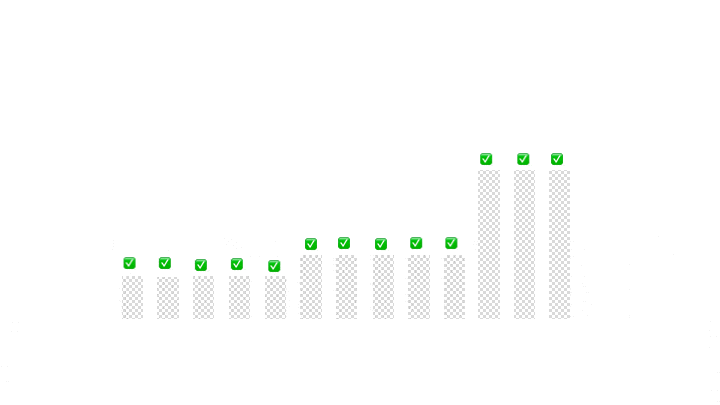
6. Анализ алгоритма

В общем, алгоритм быстрой сортировки имеет временную сложность в среднем O(n*log(n)) и временную сложность в наихудшем случае O(n ^2 ). При высокой плотности повторяющихся ключей мы почти всегда получаем наихудшую производительность при тривиальной реализации быстрой сортировки.

Однако, когда мы используем вариант быстрой сортировки с трехсторонним разделением, например разделение DNF или разделение Bentley, мы можем предотвратить негативное влияние дублирующихся ключей. Кроме того, по мере увеличения плотности повторяющихся ключей производительность нашего алгоритма также улучшается. В результате мы получаем наилучшую производительность, когда все ключи равны, и мы получаем один раздел, содержащий все одинаковые ключи за линейное время.

Тем не менее, мы должны отметить, что мы существенно увеличиваем накладные расходы, когда переключаемся на трехстороннюю схему секционирования с тривиальной схемы секционирования с одной опорной точкой.

Для подхода на основе DNF накладные расходы не зависят от плотности повторяющихся ключей. Таким образом, если мы используем разбиение DNF для массива со всеми уникальными ключами, мы получим низкую производительность по сравнению с тривиальной реализацией, в которой мы оптимально выбираем опорную точку.

Но подход Bentley-McIlroy делает умную вещь, поскольку накладные расходы на перемещение одинаковых ключей с двух крайних концов зависят от их количества. В результате, если мы используем этот алгоритм для массива со всеми уникальными ключами, даже тогда мы получим достаточно хорошую производительность.

Таким образом, временная сложность в наихудшем случае как алгоритмов разбиения с одной опорной точкой, так и алгоритмов разбиения по трем направлениям составляет O(nlog(n)) . Однако реальная выгода видна в наилучших сценариях , где мы видим, что временная сложность увеличивается от O(nlog(n)) для одноповоротного разбиения до O(n) для трехстороннего разбиения.

7. Заключение

В этом руководстве мы узнали о проблемах с производительностью при тривиальной реализации алгоритма быстрой сортировки, когда входные данные содержат большое количество повторяющихся элементов.

Желая решить эту проблему, мы изучили различные схемы трехстороннего разбиения и то, как мы можем реализовать их в Java.

Как всегда, полный исходный код реализации Java, используемой в этой статье, доступен на GitHub .