1. Введение
В этом уроке мы рассмотрим методы хеширования, используемые в различных структурах данных, которые обеспечивают постоянный доступ к своим элементам во времени.
Мы более подробно обсудим так называемую технику складывания и дадим краткое введение в технику мид-сквер и биннинг.
2. Обзор
Когда мы выбираем структуры данных для хранения объектов, одним из соображений является необходимость быстрого доступа к ним.
Пакет утилит Java предлагает нам довольно много структур данных для хранения наших объектов. Для получения дополнительной информации о структурах данных обратитесь к нашей странице компиляции коллекций Java , которая содержит руководства по некоторым из них.
Как мы знаем, некоторые из этих структур данных позволяют нам извлекать их элементы за постоянное время, независимо от количества содержащихся в них элементов.
Наверное, самым простым является массив. Фактически мы обращаемся к элементам массива по их индексу. Время доступа, естественно, не зависит от размера массива. Фактически, за кулисами многие структуры данных активно используют массивы.
Проблема в том, что индексы массива должны быть числовыми, а мы часто предпочитаем манипулировать этими структурами данных с помощью объектов.
Чтобы решить эту проблему, многие структуры данных пытаются присвоить числовое значение, которое может служить индексом массива для объектов. Мы называем это значение хеш-значением или просто хэшем .
3. Хеширование
**Хэширование — это преобразование объекта в числовое значение . ** Функции, которые выполняют эти преобразования, называются хеш-функциями .
Для простоты рассмотрим хэш-функции, преобразующие строки в индексы массива, то есть в целые числа из диапазона [0, N] с конечным N.
Естественно, хэш-функция применяется к большому количеству строк . Поэтому становятся важными его «глобальные» свойства.
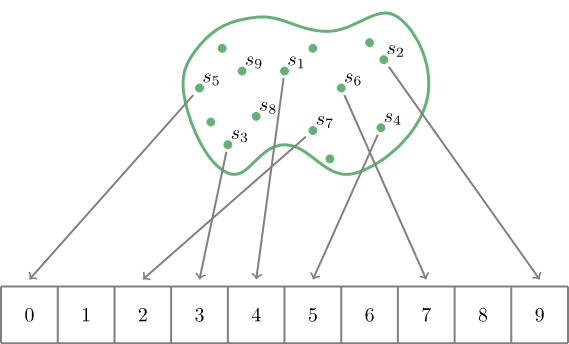
К сожалению, невозможно, чтобы хэш-функция всегда преобразовывала разные строки в разные числа .
Мы можем довольно легко убедиться, что количество строк намного больше, чем количество целых чисел в любом диапазоне [0, N] . Следовательно, неизбежно наличие пары неравных строк, для которых хэш-функция выдает равные значения. Это явление называется столкновением .
Мы не собираемся погружаться в инженерные детали хеш-функций, но ясно, что хорошая хеш-функция должна пытаться единообразно отображать строки, в которых она определена, в числа.
Другое очевидное требование состоит в том, что хорошая хэш-функция должна быть быстрой. Если вычисление хеш-значения занимает слишком много времени, мы не можем быстро получить доступ к элементам.
В этом уроке мы рассмотрим один из методов, который пытается сделать сопоставление однородным , сохраняя при этом его быстроту.
4. Техника складывания
Наша цель — найти функцию, которая преобразует строки в индексы массива. Просто чтобы проиллюстрировать идею, предположим, что мы хотим, чтобы этот массив имел емкость для 10 ^5 элементов, и давайте в качестве примера используем строковый язык Java .
4.1. Описание
Начнем с преобразования символов строки в числа. ASCII является хорошим кандидатом для этой операции:
Теперь мы объединяем числа, которые мы только что получили, в группы некоторого размера. Как правило, мы выбираем значение размера группы на основе размера нашего массива, который равен 10 ^5 . Так как числа, в которые мы преобразовали символы, содержат от двух до трех цифр, без ограничения общности можно установить размер группы равным двум:
Следующий шаг — соединить числа в каждой группе, как если бы они были строками, и найти их сумму:
Теперь мы должны сделать последний шаг. Проверим, может ли число 348933 служить индексом нашего массива размером 10 ^5 . Естественно, оно превышает максимально допустимое значение 99999. Мы можем легко решить эту проблему, применив оператор по модулю, чтобы найти окончательный результат:
348933 % 10000 = 48933
4.2. Заключительные замечания
Мы видим, что алгоритм не включает никаких трудоемких операций и, следовательно, он достаточно быстр. Каждый символ входной строки влияет на конечный результат. Этот факт определенно помогает уменьшить коллизии, но не избежать их полностью.
Например, если бы мы хотели пропустить свертывание и применить оператор по модулю непосредственно к преобразованной в ASCII строке ввода (игнорируя проблему переполнения)
749711897321089711010311797103101 % 100000 = 3101
тогда такая хэш-функция будет давать одно и то же значение для всех строк, которые имеют те же последние два символа, что и наша входная строка: a ge , page , large и т. д.
Из описания алгоритма легко увидеть, что он не свободен от коллизий. Например, алгоритм создает одно и то же значение хеш-функции для строк языка Java и языка vaJa .
5. Другие методы
Техника складывания довольно распространена, но не единственная. Иногда также могут быть полезны методы биннинга или мид-сквер .
Мы иллюстрируем их идею, используя не строки, а числа (предположим, что мы уже каким-то образом преобразовали строки в числа). Мы не будем обсуждать их преимущества и недостатки, но вы можете составить мнение, увидев алгоритмы.
5.1. Техника биннинга
Предположим, что у нас есть 100 целых чисел, и мы хотим, чтобы наша хэш-функция отображала их в массив из 10 элементов. Затем мы можем просто разбить эти 100 целых чисел на десять групп таким образом, что первые десять целых чисел окажутся в первой ячейке, вторые десять целых чисел окажутся во второй ячейке и т. д.:
5.2. Среднеквадратная техника
Этот алгоритм был предложен Джоном фон Нейманом и позволяет нам генерировать псевдослучайные числа, начиная с заданного числа.
Проиллюстрируем это на конкретном примере. Предположим, у нас есть четырехзначное число 1111 . По алгоритму возводим его в квадрат, получая таким образом 1234321 . Теперь из середины извлекаем четыре цифры, например, 2343 . Алгоритм позволяет нам повторять этот процесс, пока мы не будем удовлетворены результатом.
6. Заключение
В этом уроке мы рассмотрели несколько методов хеширования. Мы подробно описали технику фальцовки и дали краткое описание того, как можно добиться группировки и мид-квадрата.
Как всегда, мы можем найти соответствующие фрагменты кода в нашем репозитории GitHub .