1. Введение
Алгоритмы поиска пути — это методы навигации по картам , позволяющие нам найти маршрут между двумя разными точками. Разные алгоритмы имеют разные плюсы и минусы, часто с точки зрения эффективности алгоритма и эффективности генерируемого им маршрута.
2. Что такое алгоритм поиска пути?
Алгоритм поиска пути — это метод преобразования графа, состоящего из узлов и ребер, в маршрут через граф . Этот граф может быть чем угодно, что требует обхода. В этой статье мы попытаемся пройти часть системы лондонского метро:
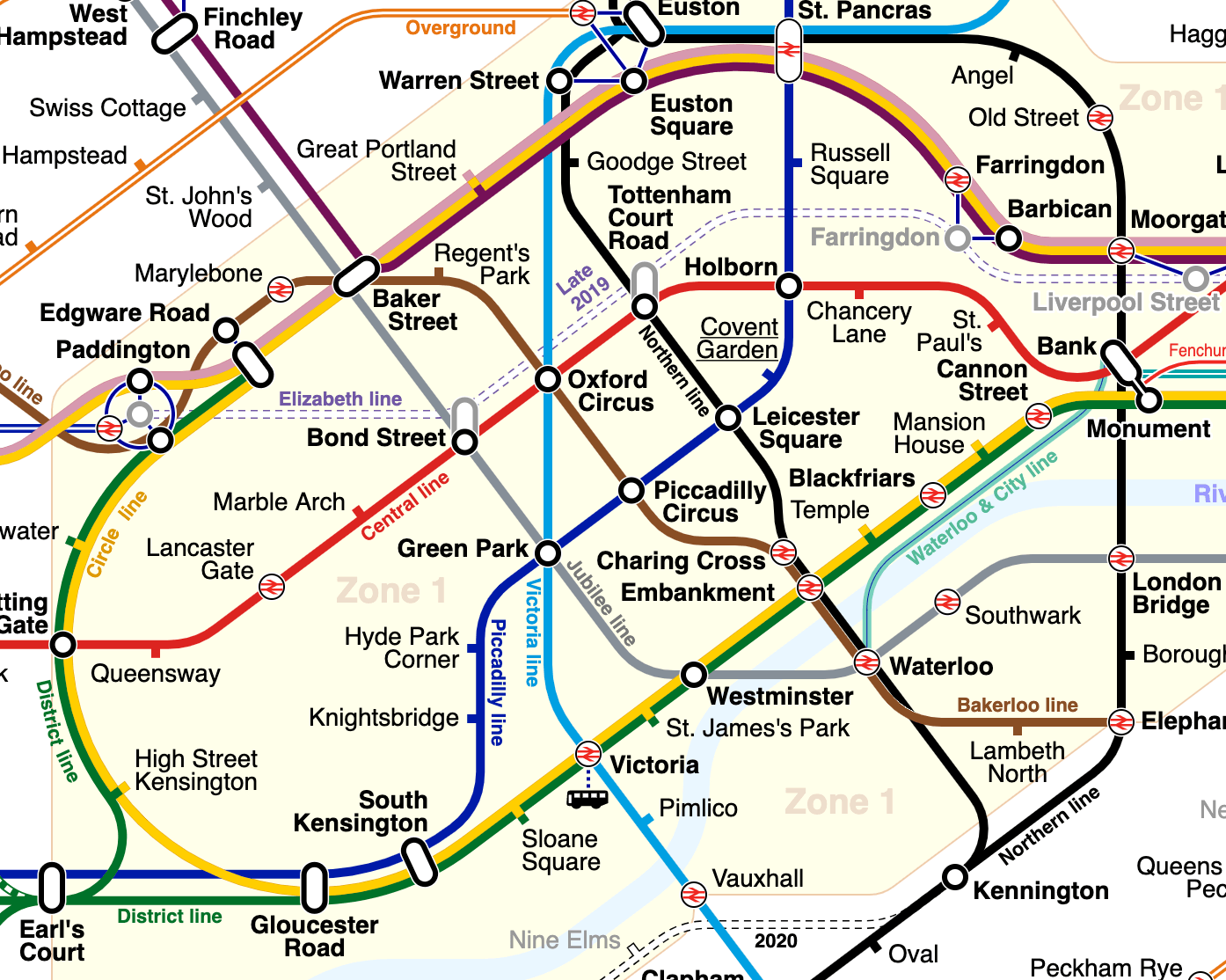
(« Карта лондонского метро Overground DLR Crossrail » от sameboat лицензирована в соответствии с CC BY-SA 4.0 )
В нем много интересных компонентов:
- У нас может быть, а может и не быть прямого маршрута между начальной и конечной точками. Например, мы можем сразу перейти от «Графского двора» к «Памятнику», но не к «Ангелу».
- Каждый шаг имеет определенную стоимость. В нашем случае это расстояние между станциями.
- Каждая остановка связана только с небольшим подмножеством других остановок. Например, «Риджентс-парк» напрямую связан только с «Бейкер-стрит» и «Оксфорд-серкус».
Все алгоритмы поиска пути принимают на вход совокупность всех узлов — в нашем случае станций — и соединений между ними, а также желаемые начальные и конечные точки. Результатом обычно является набор узлов, которые проведут нас от начала до конца в том порядке, в котором нам нужно пройти .
3. Что такое А*?
A* — это один конкретный алгоритм поиска пути , впервые опубликованный в 1968 году Питером Хартом, Нильсом Нильссоном и Бертрамом Рафаэлем. Обычно считается, что это лучший алгоритм для использования, когда нет возможности предварительно вычислить маршруты и нет ограничений на использование памяти .
Сложность как памяти, так и производительности может быть O(b^d) в худшем случае, поэтому, хотя всегда будет работать наиболее эффективный маршрут, это не всегда самый эффективный способ сделать это.
A* на самом деле является разновидностью алгоритма Дейкстры , где предоставляется дополнительная информация, помогающая выбрать следующий узел для использования. Эта дополнительная информация не обязательно должна быть идеальной — если у нас уже есть идеальная информация, поиск пути не имеет смысла. Но чем она лучше, тем лучше будет конечный результат.
4. Как работает A*?
Алгоритм A* работает путем итеративного выбора наилучшего маршрута на данный момент и попытки определить наилучший следующий шаг.
При работе с этим алгоритмом у нас есть несколько фрагментов данных, которые нам нужно отслеживать. «Открытое множество» — это все узлы, которые мы сейчас рассматриваем. Это не каждый узел в системе, а каждый узел, из которого мы можем сделать следующий шаг.
Мы также будем отслеживать текущий лучший результат, предполагаемый общий балл и текущий лучший предыдущий узел для каждого узла в системе.
В рамках этого нам нужно иметь возможность рассчитать два разных балла. Один — это оценка перехода от одного узла к другому. Второй — это эвристика, позволяющая оценить стоимость пути от любого узла до пункта назначения. Эта оценка не обязательно должна быть точной, но большая точность даст лучшие результаты. Единственное требование состоит в том, чтобы обе оценки были согласованы друг с другом, то есть они были в одних и тех же единицах измерения.
В самом начале наш открытый набор состоит из нашего начального узла, и у нас вообще нет информации о каких-либо других узлах.
На каждой итерации мы будем:
- Выберите узел из нашего открытого набора с наименьшим оценочным общим баллом.
- Удалить этот узел из открытого набора
- Добавим в открытый набор все узлы, до которых мы можем добраться из него
Когда мы делаем это, мы также обрабатываем новую оценку от этого узла к каждому новому, чтобы увидеть, является ли это улучшением того, что у нас есть до сих пор, и если это так, мы обновляем то, что мы знаем об этом узле.
Затем это повторяется до тех пор, пока узел в нашем открытом наборе с наименьшим оценочным общим баллом не станет нашим пунктом назначения, и в этой точке мы получим наш маршрут.
4.1. Рабочий пример
Например, начнем с «Мэрилебон» и попробуем найти путь к «Бонд-стрит».
В самом начале наш открытый набор состоит только из «Мэрилебон» . Это означает, что это неявно узел, для которого у нас есть лучший «оценочный общий балл».
Следующими нашими остановками может быть либо «Edgware Road» стоимостью 0,4403 км, либо «Baker Street» стоимостью 0,4153 км. Однако «Эджвар-роуд» находится в неправильном направлении, поэтому наша эвристика отсюда до пункта назначения дает оценку 1,4284 км, тогда как «Бейкер-стрит» имеет эвристическую оценку 1,0753 км.
Это означает, что после этой итерации наш открытый набор состоит из двух записей — «Edgware Road» с расчетным общим счетом 1,8687 км и «Baker Street» с расчетным общим счетом 1,4906 км.
Затем наша вторая итерация начнется с «Бейкер-стрит», так как она имеет наименьший оценочный общий балл. Отсюда нашими следующими остановками могут быть «Мэрилебон», «Св. Джонс-Вуд», «Грейт-Портленд-стрит», «Риджентс-парк» или «Бонд-стрит».
Мы не будем рассматривать все это, но давайте возьмем «Мэрилебон» в качестве интересного примера. Стоимость проезда снова составляет 0,4153 км, но это означает, что общая стоимость теперь составляет 0,8306 км. Кроме того, эвристика отсюда до пункта назначения дает оценку 1,323 км.
Это означает, что расчетная общая оценка составит 2,1536 км, что хуже , чем предыдущая оценка для этого узла. Это имеет смысл, потому что нам пришлось проделать дополнительную работу, чтобы ничего не добиться в этом случае. Это означает, что мы не будем считать этот маршрут жизнеспособным. Таким образом, детали «Мэрилебон» не обновляются, и он не добавляется обратно в открытый набор.
5. Реализация Java
Теперь, когда мы обсудили, как это работает, давайте на самом деле реализуем это. Мы собираемся создать универсальное решение, а затем внедрить код, необходимый для его работы в лондонском метро. Затем мы можем использовать его для других сценариев, реализовав только эти определенные части.
5.1. Представление графика
Во-первых, нам нужно иметь возможность представить наш граф, который мы хотим пройти. Он состоит из двух классов — отдельных узлов и графа в целом.
Мы будем представлять наши отдельные узлы с помощью интерфейса GraphNode :
public interface GraphNode {
String getId();
}
Каждый из наших узлов должен иметь идентификатор. Все остальное специфично для этого конкретного графа и не требуется для общего решения. Эти классы представляют собой простые компоненты Java Bean без специальной логики.
Затем наш общий граф представляется классом, называемым просто Graph :
public class Graph<T extends GraphNode> {
private final Set<T> nodes;
private final Map<String, Set<String>> connections;
public T getNode(String id) {
return nodes.stream()
.filter(node -> node.getId().equals(id))
.findFirst()
.orElseThrow(() -> new IllegalArgumentException("No node found with ID"));
}
public Set<T> getConnections(T node) {
return connections.get(node.getId()).stream()
.map(this::getNode)
.collect(Collectors.toSet());
}
}
Он хранит все узлы в нашем графе и знает, какие узлы к каким подключаются. Затем мы можем получить любой узел по идентификатору или все узлы, подключенные к данному узлу.
На данный момент мы можем представить любую форму графа, какую пожелаем, с любым количеством ребер между любым количеством узлов.
5.2. Шаги на нашем пути
Следующее, что нам нужно, это наш механизм поиска маршрутов через граф.
Первая часть — это какой-то способ сгенерировать оценку между любыми двумя узлами. Мы создадим интерфейс Scorer как для оценки следующего узла, так и для оценки места назначения:
public interface Scorer<T extends GraphNode> {
double computeCost(T from, T to);
}
Имея начальный и конечный узлы, мы затем получаем оценку за перемещение между ними.
Нам также нужна оболочка вокруг наших узлов, несущая некоторую дополнительную информацию. Вместо того, чтобы быть GraphNode , это RouteNode — потому что это узел в нашем вычисляемом маршруте, а не во всем графе:
class RouteNode<T extends GraphNode> implements Comparable<RouteNode> {
private final T current;
private T previous;
private double routeScore;
private double estimatedScore;
RouteNode(T current) {
this(current, null, Double.POSITIVE_INFINITY, Double.POSITIVE_INFINITY);
}
RouteNode(T current, T previous, double routeScore, double estimatedScore) {
this.current = current;
this.previous = previous;
this.routeScore = routeScore;
this.estimatedScore = estimatedScore;
}
}
Как и в случае с GraphNode , это простые Java Beans, используемые для хранения текущего состояния каждого узла для текущего вычисления маршрута. Мы дали этому простой конструктор для общего случая, когда мы впервые посещаем узел и еще не имеем о нем дополнительной информации.
Однако они также должны быть сопоставимы , чтобы мы могли упорядочить их по оценочной оценке как части алгоритма. Это означает добавление метода compareTo() для выполнения требований интерфейса Comparable :
@Override
public int compareTo(RouteNode other) {
if (this.estimatedScore > other.estimatedScore) {
return 1;
} else if (this.estimatedScore < other.estimatedScore) {
return -1;
} else {
return 0;
}
}
5.3. Поиск нашего маршрута
Теперь мы можем фактически генерировать наши маршруты по нашему графу. Это будет класс RouteFinder :
public class RouteFinder<T extends GraphNode> {
private final Graph<T> graph;
private final Scorer<T> nextNodeScorer;
private final Scorer<T> targetScorer;
public List<T> findRoute(T from, T to) {
throw new IllegalStateException("No route found");
}
}
У нас есть граф, по которому мы находим маршруты, и два наших счетчика — один для точного счета для следующего узла, а другой для предполагаемого счета до нашего пункта назначения. У нас также есть метод, который берет начальный и конечный узлы и вычисляет лучший маршрут между ними.
Этот метод должен стать нашим алгоритмом A*. Весь остальной код находится внутри этого метода.
Мы начинаем с некоторой базовой настройки — нашего «открытого набора» узлов, которые мы можем рассматривать как следующий шаг, и карты каждого узла, который мы посетили до сих пор, и того, что мы знаем о нем:
Queue<RouteNode> openSet = new PriorityQueue<>();
Map<T, RouteNode<T>> allNodes = new HashMap<>();
RouteNode<T> start = new RouteNode<>(from, null, 0d, targetScorer.computeCost(from, to));
openSet.add(start);
allNodes.put(from, start);
Наш открытый набор изначально имеет единственный узел — нашу начальную точку . Для этого нет предыдущего узла, есть оценка 0, чтобы добраться туда, и у нас есть оценка того, как далеко он находится от пункта назначения.
Использование PriorityQueue для открытого набора означает, что мы автоматически получаем из него лучшую запись на основе нашего метода compareTo() из предыдущего.
Теперь мы повторяем до тех пор, пока либо у нас не закончатся узлы для просмотра, либо лучший доступный узел не станет нашим пунктом назначения:
while (!openSet.isEmpty()) {
RouteNode<T> next = openSet.poll();
if (next.getCurrent().equals(to)) {
List<T> route = new ArrayList<>();
RouteNode<T> current = next;
do {
route.add(0, current.getCurrent());
current = allNodes.get(current.getPrevious());
} while (current != null);
return route;
}
// ...
Когда мы нашли пункт назначения, мы можем построить наш маршрут, многократно просматривая предыдущий узел, пока не достигнем нашей начальной точки.
Далее, если мы не достигли пункта назначения, мы можем решить, что делать дальше:
graph.getConnections(next.getCurrent()).forEach(connection -> {
RouteNode<T> nextNode = allNodes.getOrDefault(connection, new RouteNode<>(connection));
allNodes.put(connection, nextNode);
double newScore = next.getRouteScore() + nextNodeScorer.computeCost(next.getCurrent(), connection);
if (newScore < nextNode.getRouteScore()) {
nextNode.setPrevious(next.getCurrent());
nextNode.setRouteScore(newScore);
nextNode.setEstimatedScore(newScore + targetScorer.computeCost(connection, to));
openSet.add(nextNode);
}
});
throw new IllegalStateException("No route found");
}
Здесь мы перебираем подключенные узлы из нашего графа. Для каждого из них мы получаем RouteNode , который у нас есть для него — при необходимости создаем новый.
Затем мы вычисляем новую оценку для этого узла и смотрим, дешевле ли она, чем была до сих пор. Если это так, мы обновляем его, чтобы он соответствовал этому новому маршруту, и добавляем его в открытый набор для рассмотрения в следующий раз.
Это весь алгоритм. Мы продолжаем повторять это до тех пор, пока либо не достигнем своей цели, либо не достигнем ее.
5.4. Конкретные сведения о лондонском метро
То, что у нас есть до сих пор, — это общий поиск пути A*, но ему не хватает специфики, необходимой для нашего конкретного варианта использования. Это означает, что нам нужна конкретная реализация как GraphNode, так и Scorer .
Наши узлы — это станции метро, и мы будем моделировать их с помощью класса Station :
public class Station implements GraphNode {
private final String id;
private final String name;
private final double latitude;
private final double longitude;
}
Имя полезно для просмотра вывода, а широта и долгота — для оценки.
В этом сценарии нам нужна только одна реализация Scorer . Мы собираемся использовать для этого формулу Хаверсина , чтобы вычислить расстояние по прямой между двумя парами широта/долгота:
public class HaversineScorer implements Scorer<Station> {
@Override
public double computeCost(Station from, Station to) {
double R = 6372.8; // Earth's Radius, in kilometers
double dLat = Math.toRadians(to.getLatitude() - from.getLatitude());
double dLon = Math.toRadians(to.getLongitude() - from.getLongitude());
double lat1 = Math.toRadians(from.getLatitude());
double lat2 = Math.toRadians(to.getLatitude());
double a = Math.pow(Math.sin(dLat / 2),2)
+ Math.pow(Math.sin(dLon / 2),2) * Math.cos(lat1) * Math.cos(lat2);
double c = 2 * Math.asin(Math.sqrt(a));
return R * c;
}
}
Теперь у нас есть почти все необходимое для расчета путей между любыми двумя парами станций. Не хватает только графика связей между ними. Это доступно на GitHub .
Давайте использовать его для составления маршрута. Мы создадим один из Earl's Court до Angel. У него есть несколько различных вариантов проезда как минимум по двум линиям метро:
public void findRoute() {
List<Station> route = routeFinder.findRoute(underground.getNode("74"), underground.getNode("7"));
System.out.println(route.stream().map(Station::getName).collect(Collectors.toList()));
}
Это генерирует маршрут Earl's Court -> South Kensington -> Green Park -> Euston -> Angel.
Очевидным маршрутом, по которому пошли бы многие люди, скорее всего, был бы Earl's Count -> Monument -> Angel, потому что там меньше изменений. Вместо этого это пошло значительно более прямым путем, хотя это означало больше изменений.
6. Заключение
В этой статье мы увидели, что такое алгоритм A*, как он работает и как его реализовать в наших собственных проектах. Почему бы не взять это и не расширить для собственного использования?
Может быть, попробовать расширить его, чтобы учесть развязки между линиями метро, и посмотреть, как это повлияет на выбранные маршруты?
И снова полный код статьи доступен на GitHub .