1. Обзор
В этом уроке мы разберемся с основными понятиями графа как структуры данных .
Мы также рассмотрим его реализацию на Java вместе с различными операциями, возможными на графе. Мы также обсудим библиотеки Java, предлагающие реализации графов.
2. Структура графических данных
Граф — это структура данных для хранения связанных данных , таких как сеть людей на платформе социальных сетей.
Граф состоит из вершин и ребер. Вершина представляет объект (например, людей), а ребро представляет отношения между объектами (например, дружеские отношения человека).
Давайте определим простой график, чтобы понять это лучше:
Здесь мы определили простой граф с пятью вершинами и шестью ребрами. Круги — это вершины, представляющие людей, а линии, соединяющие две вершины, — это ребра, представляющие друзей на онлайн-портале.
Есть несколько вариантов этого простого графа в зависимости от свойств ребер. Давайте кратко рассмотрим их в следующих разделах.
Однако мы сосредоточимся только на простом графике, представленном здесь для примеров Java в этом руководстве.
2.1. Направленный граф
Граф, который мы определили до сих пор, имеет ребра без какого-либо направления. Если эти ребра имеют направление в них , результирующий граф известен как ориентированный граф .
Примером этого может быть представление того, кто отправляет запрос на добавление в друзья на онлайн-портале:
Здесь мы видим, что ребра имеют фиксированное направление. Края также могут быть двунаправленными.
2.2. Взвешенный график
Опять же, наш простой граф имеет несмещенные или невзвешенные ребра. Если вместо этого эти ребра имеют относительный вес , этот граф известен как взвешенный граф.
Примером практического применения этого может быть представление того, насколько относительно стара дружба на онлайн-портале:
Здесь мы видим, что ребра имеют связанные с ними веса. Это обеспечивает относительное значение этих краев.
3. Графические представления
Граф может быть представлен в различных формах, таких как матрица смежности и список смежности. У каждого есть свои плюсы и минусы в разных настройках.
Мы представим эти графовые представления в этом разделе.
3.1. Матрица смежности
Матрица смежности — это квадратная матрица с размерами, эквивалентными количеству вершин в графе.
Элементы матрицы обычно имеют значения «0» или «1». Значение «1» указывает на смежность между вершинами в строке и столбце, а значение «0» — в противном случае.
Давайте посмотрим, как выглядит матрица смежности для нашего простого графа из предыдущего раздела:
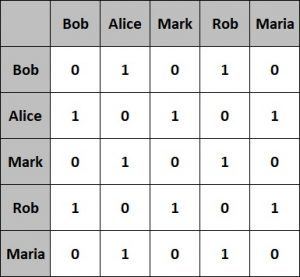
Это представление довольно легко реализовать, а также эффективно запрашивать. Однако он менее эффективен по отношению к занимаемому пространству .
3.2. Список смежности
Список смежности — это не что иное , как массив списков . Размер массива эквивалентен количеству вершин в графе.
Список по определенному индексу массива представляет смежные вершины вершины, представленной этим индексом массива.
Давайте посмотрим, как выглядит список смежности для нашего простого графа из предыдущего раздела:
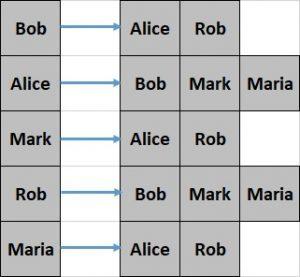
Такое представление сравнительно сложно создать и менее эффективно запрашивать . Тем не менее, он предлагает лучшую эффективность использования пространства .
Мы будем использовать список смежности для представления графа в этом руководстве.
4. Графики в Java
В Java нет стандартной реализации структуры данных графа.
Однако мы можем реализовать граф с помощью коллекций Java.
Начнем с определения вершины:
class Vertex {
String label;
Vertex(String label) {
this.label = label;
}
// equals and hashCode
}
Приведенное выше определение вершины содержит только метку, но она может представлять любую возможную сущность, такую как Человек или Город.
Также обратите внимание, что мы должны переопределить методы equals() и hashCode() , поскольку они необходимы для работы с коллекциями Java.
Как мы обсуждали ранее, граф — это не что иное, как набор вершин и ребер, которые могут быть представлены либо в виде матрицы смежности, либо в виде списка смежности.
Давайте посмотрим, как мы можем определить это, используя список смежности здесь:
class Graph {
private Map<Vertex, List<Vertex>> adjVertices;
// standard constructor, getters, setters
}
Как мы видим здесь, класс Graph использует Map from Java Collections для определения списка смежности.
В структуре данных графа возможно несколько операций, таких как создание, обновление или поиск по графу .
Мы рассмотрим некоторые из наиболее распространенных операций и посмотрим, как мы можем реализовать их в Java.
5. Операции изменения графа
Для начала мы определим несколько методов для изменения структуры данных графа.
Давайте определим методы для добавления и удаления вершин:
void addVertex(String label) {
adjVertices.putIfAbsent(new Vertex(label), new ArrayList<>());
}
void removeVertex(String label) {
Vertex v = new Vertex(label);
adjVertices.values().stream().forEach(e -> e.remove(v));
adjVertices.remove(new Vertex(label));
}
Эти методы просто добавляют и удаляют элементы из набора вершин .
Теперь давайте также определим метод для добавления ребра:
void addEdge(String label1, String label2) {
Vertex v1 = new Vertex(label1);
Vertex v2 = new Vertex(label2);
adjVertices.get(v1).add(v2);
adjVertices.get(v2).add(v1);
}
Этот метод создает новый край и обновляет карту соседних вершин . ``
Аналогичным образом мы определим метод removeEdge() :
void removeEdge(String label1, String label2) {
Vertex v1 = new Vertex(label1);
Vertex v2 = new Vertex(label2);
List<Vertex> eV1 = adjVertices.get(v1);
List<Vertex> eV2 = adjVertices.get(v2);
if (eV1 != null)
eV1.remove(v2);
if (eV2 != null)
eV2.remove(v1);
}
Теперь давайте посмотрим, как мы можем создать простой график, который мы нарисовали ранее, используя методы, которые мы определили до сих пор:
Graph createGraph() {
Graph graph = new Graph();
graph.addVertex("Bob");
graph.addVertex("Alice");
graph.addVertex("Mark");
graph.addVertex("Rob");
graph.addVertex("Maria");
graph.addEdge("Bob", "Alice");
graph.addEdge("Bob", "Rob");
graph.addEdge("Alice", "Mark");
graph.addEdge("Rob", "Mark");
graph.addEdge("Alice", "Maria");
graph.addEdge("Rob", "Maria");
return graph;
}
Наконец, мы определим метод для получения смежных вершин конкретной вершины:
List<Vertex> getAdjVertices(String label) {
return adjVertices.get(new Vertex(label));
}
6. Обход графика
Теперь, когда у нас есть структура данных графа и функции для ее создания и обновления, мы можем определить некоторые дополнительные функции для обхода графа. Нам нужно пройти по графу, чтобы выполнить какое-либо осмысленное действие, например поиск по графу.
Существует два возможных способа обхода графа: обход в глубину и обход в ширину .
6.1. Обход в глубину
Обход в глубину начинается с произвольной корневой вершины и исследует вершины как можно глубже вдоль каждой ветви, прежде чем исследовать вершины того же уровня .
Давайте определим метод для выполнения обхода в глубину:
Set<String> depthFirstTraversal(Graph graph, String root) {
Set<String> visited = new LinkedHashSet<String>();
Stack<String> stack = new Stack<String>();
stack.push(root);
while (!stack.isEmpty()) {
String vertex = stack.pop();
if (!visited.contains(vertex)) {
visited.add(vertex);
for (Vertex v : graph.getAdjVertices(vertex)) {
stack.push(v.label);
}
}
}
return visited;
}
Здесь мы используем стек для хранения вершин, которые необходимо пройти .
Давайте запустим это на графике, который мы создали в предыдущем подразделе:
assertEquals("[Bob, Rob, Maria, Alice, Mark]", depthFirstTraversal(graph, "Bob").toString());
Обратите внимание, что здесь мы используем вершину «Боб» в качестве корня для обхода, но это может быть любая другая вершина.
6.2. Обход в ширину
Для сравнения, обход в ширину начинается с произвольной корневой вершины и исследует все соседние вершины на том же уровне, прежде чем углубляться в граф.
Теперь давайте определим метод для выполнения обхода в ширину:
Set<String> breadthFirstTraversal(Graph graph, String root) {
Set<String> visited = new LinkedHashSet<String>();
Queue<String> queue = new LinkedList<String>();
queue.add(root);
visited.add(root);
while (!queue.isEmpty()) {
String vertex = queue.poll();
for (Vertex v : graph.getAdjVertices(vertex)) {
if (!visited.contains(v.label)) {
visited.add(v.label);
queue.add(v.label);
}
}
}
return visited;
}
Обратите внимание, что обход в ширину использует Queue для хранения вершин, которые необходимо пройти .
Снова запустим этот обход на том же графе:
assertEquals(
"[Bob, Alice, Rob, Mark, Maria]", breadthFirstTraversal(graph, "Bob").toString());
Опять же, корневая вершина, которой здесь является «Боб», может быть любой другой вершиной.
7. Библиотеки Java для графиков
Нет необходимости всегда реализовывать граф с нуля в Java. Доступно несколько библиотек с открытым исходным кодом и зрелых библиотек, которые предлагают реализации графов.
В следующих нескольких подразделах мы рассмотрим некоторые из этих библиотек.
7.1. JGraphT
JGraphT — одна из самых популярных библиотек в Java для построения структуры данных графа. Он позволяет создавать простой граф, ориентированный граф, взвешенный граф и другие.
Кроме того, он предлагает множество возможных алгоритмов для структуры данных графа. В одном из наших предыдущих руководств JGraphT рассматривается более подробно .
7.2. Google Гуава
Google Guava — это набор библиотек Java, которые предлагают ряд функций, включая структуру данных графа и его алгоритмы.
Он поддерживает создание простого Graph , ValueGraph и Network . Они могут быть определены как Mutable или Immutable .
7.3. Апач Коммонс
Apache Commons — это проект Apache, предлагающий многоразовые компоненты Java. Это включает в себя Commons Graph, который предлагает набор инструментов для создания и управления структурой данных графа. Это также обеспечивает общие алгоритмы графа для работы со структурой данных.
7.4. SourceForge JUNG
Java Universal Network/Graph (JUNG) — это платформа Java, предоставляющая расширяемый язык для моделирования, анализа и визуализации любых данных, которые могут быть представлены в виде графика.
JUNG поддерживает ряд алгоритмов, которые включают в себя такие процедуры, как кластеризация, декомпозиция и оптимизация.
Эти библиотеки предоставляют ряд реализаций, основанных на структуре данных графа. Существуют также более мощные фреймворки, основанные на графах , такие как Apache Giraph , который в настоящее время используется в Facebook для анализа графа, формируемого их пользователями, и Apache TinkerPop , обычно используемый поверх графовых баз данных.
8. Заключение
В этой статье мы обсудили граф как структуру данных вместе с ее представлениями. Мы определили очень простой граф в Java с помощью коллекций Java, а также определили общие обходы для графа.
Мы также кратко рассказали о различных библиотеках, доступных в Java за пределами платформы Java, которые обеспечивают реализацию графов.
Как всегда, код примеров доступен на GitHub .