Введение в JGraphT

1. Обзор

В большинстве случаев, когда мы реализуем алгоритмы на основе графов, нам также необходимо реализовать некоторые служебные функции.

JGraphT — это библиотека классов Java с открытым исходным кодом, которая не только предоставляет нам различные типы графиков, но и множество полезных алгоритмов для решения наиболее часто встречающихся проблем с графами.

В этой статье мы увидим, как создавать разные типы графиков и насколько удобно пользоваться предоставленными утилитами.

2. Зависимость от Maven

Давайте начнем с добавления зависимости в наш проект Maven:

<dependency>
    <groupId>org.jgrapht</groupId>
    <artifactId>jgrapht-core</artifactId>
    <version>1.0.1</version>
</dependency>

Последнюю версию можно найти на Maven Central .

3. Создание графиков

JGraphT поддерживает различные типы графиков.

3.1. Простые графики

Для начала создадим простой граф с вершиной типа String :

Graph<String, DefaultEdge> g 
  = new SimpleGraph<>(DefaultEdge.class);
g.addVertex(“v1”);
g.addVertex(“v2”);
g.addEdge(v1, v2);

3.2. Направленные/неориентированные графы

Это также позволяет нам создавать ориентированные/неориентированные графы.

В нашем примере мы создадим ориентированный граф и будем использовать его для демонстрации других полезных функций и алгоритмов:

DirectedGraph<String, DefaultEdge> directedGraph 
  = new DefaultDirectedGraph<>(DefaultEdge.class);
directedGraph.addVertex("v1");
directedGraph.addVertex("v2");
directedGraph.addVertex("v3");
directedGraph.addEdge("v1", "v2");
// Add remaining vertices and edges

3.3. Полные графики

Точно так же мы можем сгенерировать полный граф:

public void createCompleteGraph() {
    completeGraph = new SimpleWeightedGraph<>(DefaultEdge.class);
    CompleteGraphGenerator<String, DefaultEdge> completeGenerator 
      = new CompleteGraphGenerator<>(size);
    VertexFactory<String> vFactory = new VertexFactory<String>() {
        private int id = 0;
        public String createVertex() {
            return "v" + id++;
        }
    };
    completeGenerator.generateGraph(completeGraph, vFactory, null);
}

3.4. Мультиграфы

Помимо простых графов API также предоставляет нам мультиграфы (графы с несколькими путями между двумя вершинами).

Кроме того, у нас могут быть взвешенные/невзвешенные или определяемые пользователем ребра в любом графе.

Создадим мультиграф со взвешенными ребрами:

public void createMultiGraphWithWeightedEdges() {
    multiGraph = new Multigraph<>(DefaultWeightedEdge.class);
    multiGraph.addVertex("v1");
    multiGraph.addVertex("v2");
    DefaultWeightedEdge edge1 = multiGraph.addEdge("v1", "v2");
    multiGraph.setEdgeWeight(edge1, 5);

    DefaultWeightedEdge edge2 = multiGraph.addEdge("v1", "v2");
    multiGraph.setEdgeWeight(edge2, 3);
}

В дополнение к этому у нас могут быть немодифицируемые (только для чтения) и прослушиваемые (позволяет внешним слушателям отслеживать модификации) графы, а также подграфы. Также мы всегда можем создать все композиции этих графиков.

Дополнительные сведения об API можно найти здесь .

4. Алгоритмы API

Теперь, когда у нас есть полноценные графовые объекты, давайте рассмотрим некоторые распространенные проблемы и их решения.

4.1. Итерация графика

Мы можем перемещаться по графу, используя различные итераторы, такие как BreadthFirstIterator , DepthFirstIterator , ClosestFirstIterator , RandomWalkIterator в соответствии с требованиями.

Нам просто нужно создать экземпляр соответствующих итераторов, передав объекты графа:

DepthFirstIterator depthFirstIterator 
  = new DepthFirstIterator<>(directedGraph);
BreadthFirstIterator breadthFirstIterator 
  = new BreadthFirstIterator<>(directedGraph);

Как только мы получим объекты итератора, мы можем выполнить итерацию, используя методы hasNext() и next() .

4.2. Поиск кратчайшего пути

Он предоставляет реализации различных алгоритмов, таких как Dijkstra, Bellman-Ford, Astar и FloydWarshall, в пакете org.jgrapht.alg.shortestpath .

Найдем кратчайший путь по алгоритму Дейкстры:

@Test
public void whenGetDijkstraShortestPath_thenGetNotNullPath() {
    DijkstraShortestPath dijkstraShortestPath 
      = new DijkstraShortestPath(directedGraph);
    List<String> shortestPath = dijkstraShortestPath
      .getPath("v1","v4").getVertexList();
 
    assertNotNull(shortestPath);
}

Точно так же, чтобы получить кратчайший путь с помощью алгоритма Беллмана-Форда:

@Test
public void 
  whenGetBellmanFordShortestPath_thenGetNotNullPath() {
    BellmanFordShortestPath bellmanFordShortestPath 
      = new BellmanFordShortestPath(directedGraph);
    List<String> shortestPath = bellmanFordShortestPath
      .getPath("v1", "v4")
      .getVertexList();
 
    assertNotNull(shortestPath);
}

4.3. Поиск сильно связанных подграфов

Прежде чем мы перейдем к реализации, давайте кратко рассмотрим, что означают сильно связанные подграфы. Подграф называется сильно связным, только если существует путь между каждой парой его вершин.

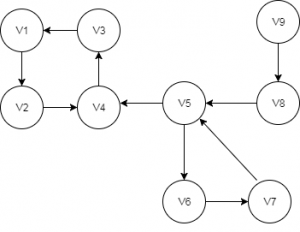
В нашем примере {v1,v2,v3,v4} можно считать сильно связным подграфом, если мы можем пройти к любой вершине независимо от текущей вершины.

Мы можем перечислить четыре таких подграфа для ориентированного графа, показанного на изображении выше:

{v9},{v8},{v5,v6,v7},{v1,v2,v3,v4}.

Реализация для перечисления всех сильно связанных подграфов:

@Test
public void 
  whenGetStronglyConnectedSubgraphs_thenPathExists() {

    StrongConnectivityAlgorithm<String, DefaultEdge> scAlg 
      = new KosarajuStrongConnectivityInspector<>(directedGraph);
    List<DirectedSubgraph<String, DefaultEdge>> stronglyConnectedSubgraphs 
      = scAlg.stronglyConnectedSubgraphs();
    List<String> stronglyConnectedVertices 
      = new ArrayList<>(stronglyConnectedSubgraphs.get(3)
      .vertexSet());

    String randomVertex1 = stronglyConnectedVertices.get(0);
    String randomVertex2 = stronglyConnectedVertices.get(3);
    AllDirectedPaths<String, DefaultEdge> allDirectedPaths 
      = new AllDirectedPaths<>(directedGraph);

    List<GraphPath<String, DefaultEdge>> possiblePathList 
      = allDirectedPaths.getAllPaths(
        randomVertex1, randomVertex2, false,
          stronglyConnectedVertices.size());
 
    assertTrue(possiblePathList.size() > 0);
}

4.4. Эйлерова схема

Эйлерова цепь в графе G — это цепь, включающая все вершины и ребра графа G. Граф, в котором он есть, является эйлеровым графом.

Давайте посмотрим на график:

public void createGraphWithEulerianCircuit() {
    SimpleWeightedGraph<String, DefaultEdge> simpleGraph 
      = new SimpleWeightedGraph<>(DefaultEdge.class);
    IntStream.range(1,5)
      .forEach(i-> simpleGraph.addVertex("v" + i));
    IntStream.range(1,5)
      .forEach(i-> {
        int endVertexNo = (i + 1) > 5 ? 1 : i + 1;
        simpleGraph.addEdge("v" + i,"v" + endVertexNo);
    });
}

Теперь мы можем проверить, содержит ли граф эйлеров цикл, используя API:

@Test
public void givenGraph_whenCheckEluerianCycle_thenGetResult() {
    HierholzerEulerianCycle eulerianCycle 
      = new HierholzerEulerianCycle<>();
 
    assertTrue(eulerianCycle.isEulerian(simpleGraph));
}
@Test
public void whenGetEulerianCycle_thenGetGraphPath() {
    HierholzerEulerianCycle eulerianCycle 
      = new HierholzerEulerianCycle<>();
    GraphPath path = eulerianCycle.getEulerianCycle(simpleGraph);
 
    assertTrue(path.getEdgeList()
      .containsAll(simpleGraph.edgeSet()));
}

4.5. Гамильтонов контур

GraphPath , который посещает каждую вершину ровно один раз, называется гамильтоновым путем.

Гамильтонов цикл (или гамильтонова цепь) — это гамильтонов путь такой, что существует ребро (в графе) от последней вершины до первой вершины пути.

Мы можем найти оптимальный гамильтонов цикл для полного графа с помощью метода HamiltonianCycle.getApproximateOptimalForCompleteGraph() .

Этот метод вернет приблизительный минимальный тур коммивояжера (гамильтоновский цикл). Оптимальное решение является NP-полным, так что это хорошее приближение, работающее за полиномиальное время:

public void 
  whenGetHamiltonianCyclePath_thenGetVerticeSequence() {
    List<String> verticeList = HamiltonianCycle
      .getApproximateOptimalForCompleteGraph(completeGraph);
 
    assertEquals(verticeList.size(), completeGraph.vertexSet().size());
}

4.6. Детектор циклов

Мы также можем проверить, есть ли циклы в графе. В настоящее время CycleDetector поддерживает только ориентированные графы:

@Test
public void whenCheckCycles_thenDetectCycles() {
    CycleDetector<String, DefaultEdge> cycleDetector 
      = new CycleDetector<String, DefaultEdge>(directedGraph);
 
    assertTrue(cycleDetector.detectCycles());
    Set<String> cycleVertices = cycleDetector.findCycles();
 
    assertTrue(cycleVertices.size() > 0);
}

5. Визуализация графика

JGraphT позволяет нам генерировать визуализации графиков и сохранять их как изображения , сначала добавим зависимость расширения jgrapht-ext от Maven Central:

<dependency>
    <groupId>org.jgrapht</groupId>
    <artifactId>jgrapht-ext</artifactId>
    <version>1.0.1</version>
</dependency>

Далее создадим простой ориентированный граф с 3 вершинами и 3 ребрами:

@Before
public void createGraph() {

    File imgFile = new File("src/test/resources/graph.png");
    imgFile.createNewFile();

    DefaultDirectedGraph<String, DefaultEdge> g = 
      new DefaultDirectedGraph<String, DefaultEdge>(DefaultEdge.class);

    String x1 = "x1";
    String x2 = "x2";
    String x3 = "x3";

    g.addVertex(x1);
    g.addVertex(x2);
    g.addVertex(x3);

    g.addEdge(x1, x2);
    g.addEdge(x2, x3);
    g.addEdge(x3, x1);
}

Теперь мы можем визуализировать этот график:

@Test
public void givenAdaptedGraph_whenWriteBufferedImage_thenFileShouldExist() throws IOException {

    JGraphXAdapter<String, DefaultEdge> graphAdapter = 
      new JGraphXAdapter<String, DefaultEdge>(g);
    mxIGraphLayout layout = new mxCircleLayout(graphAdapter);
    layout.execute(graphAdapter.getDefaultParent());
    
    BufferedImage image = 
      mxCellRenderer.createBufferedImage(graphAdapter, null, 2, Color.WHITE, true, null);
    File imgFile = new File("src/test/resources/graph.png");
    ImageIO.write(image, "PNG", imgFile);

    assertTrue(imgFile.exists());
}

Здесь мы создали JGraphXAdapter , который получает наш график в качестве аргумента конструктора, и мы применили к нему mxCircleLayout . Это выстраивает визуализацию по кругу.

Кроме того, мы используем mxCellRenderer для создания BufferedImage , а затем записываем визуализацию в файл png.

Мы можем увидеть финальное изображение в браузере или в нашем любимом рендерере:

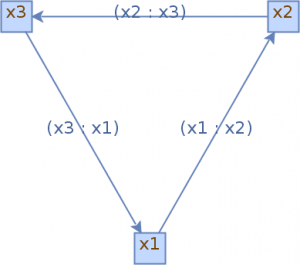
Более подробную информацию мы можем найти в официальной документации .

6. Заключение

JGraphT предоставляет практически все типы графов и множество алгоритмов графов. Мы рассмотрели, как использовать несколько популярных API. Впрочем, вы всегда можете изучить библиотеку на официальной странице .

Реализацию всех этих примеров и фрагментов кода можно найти на Github .