1. Введение
В этом уроке мы рассмотрим алгоритмы интерполяционного поиска и обсудим их плюсы и минусы. Кроме того, мы реализуем его на Java и поговорим о временной сложности алгоритма.
2. Мотивация
Поиск с интерполяцией — это усовершенствование бинарного поиска , предназначенное для равномерно распределенных данных.
Двоичный поиск разделяет пространство поиска на каждом шаге независимо от распределения данных, поэтому его временная сложность всегда равна O(log(n)) .
С другой стороны, сложность времени поиска интерполяции зависит от распределения данных . Это быстрее, чем бинарный поиск для равномерно распределенных данных с временной сложностью O(log(log(n))) . Однако в худшем случае он может работать так же плохо, как O(n) .
3. Интерполяционный поиск
Подобно бинарному поиску, интерполяционный поиск может работать только с отсортированным массивом. Он помещает зонд в рассчитанное положение на каждой итерации. Если зонд находится прямо на искомом элементе, позиция будет возвращена; в противном случае пространство поиска будет ограничено либо правой, либо левой стороной зонда.
Вычисление положения зонда — единственное различие между бинарным поиском и поиском с интерполяцией.
В бинарном поиске позиция зонда всегда является самым средним элементом оставшегося пространства поиска.
Напротив, поиск с интерполяцией вычисляет положение зонда на основе этой формулы:
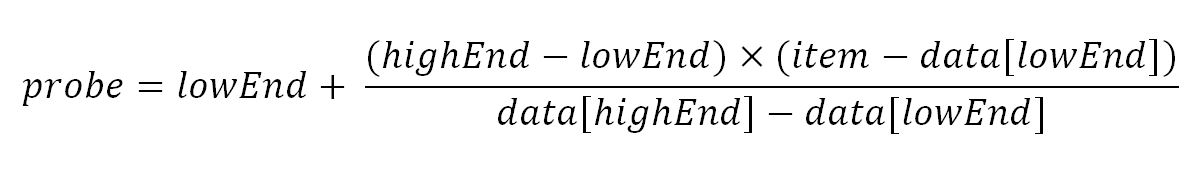
Рассмотрим каждое из условий:
probe: этому параметру будет присвоено новое положение датчика.lowEnd: индекс самого левого элемента в текущей области поиска.highEnd: индекс самого правого элемента в текущей области поиска.data[]: массив, содержащий исходное пространство поиска.item: предмет, который мы ищем.
Чтобы лучше понять, как работает интерполяционный поиск, давайте продемонстрируем его на примере.
Допустим, мы хотим найти позицию 84 в массиве ниже:
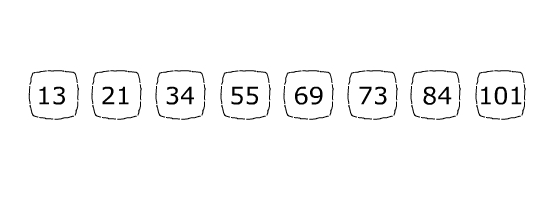
Длина массива равна 8, поэтому изначально highEnd = 7 и lowEnd = 0 (поскольку индекс массива начинается с 0, а не с 1).
На первом шаге формула положения зонда даст зонд = 5:
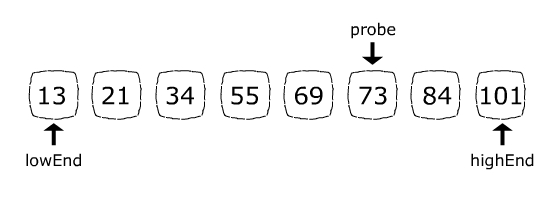
Поскольку 84 ( элемент , который мы ищем) больше, чем 73 (текущий элемент позиции зонда ), на следующем шаге мы откажемся от левой части массива, назначив lowEnd = зонд + 1. Теперь пространство поиска состоит только из 84 и 101. Формула положения датчика установит probe = 6, что точно соответствует индексу 84:
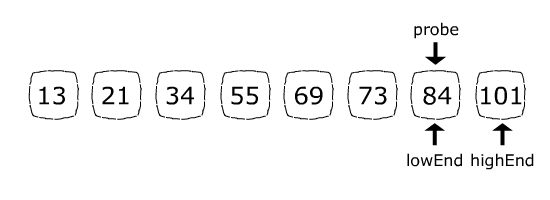
Поскольку искомый элемент найден, будет возвращена позиция 6.
4. Реализация на Java
Теперь, когда мы поняли, как работает алгоритм, давайте реализуем его на Java.
Во- первых, мы инициализируем lowEnd и highEnd :
int highEnd = (data.length - 1);
int lowEnd = 0;
Затем мы настраиваем цикл и на каждой итерации вычисляем новый зонд на основе вышеупомянутой формулы. Условие цикла гарантирует, что мы не выходим за пределы области поиска, сравнивая item с data[lowEnd] и data[highEnd] :
while (item >= data[lowEnd] && item <= data[highEnd] && lowEnd <= highEnd) {
int probe
= lowEnd + (highEnd - lowEnd) * (item - data[lowEnd]) / (data[highEnd] - data[lowEnd]);
}
Мы также проверяем, нашли ли мы предмет после каждого нового задания зонда .
Наконец, мы настраиваем lowEnd или highEnd , чтобы уменьшить пространство поиска на каждой итерации:
public int interpolationSearch(int[] data, int item) {
int highEnd = (data.length - 1);
int lowEnd = 0;
while (item >= data[lowEnd] && item <= data[highEnd] && lowEnd <= highEnd) {
int probe
= lowEnd + (highEnd - lowEnd) * (item - data[lowEnd]) / (data[highEnd] - data[lowEnd]);
if (highEnd == lowEnd) {
if (data[lowEnd] == item) {
return lowEnd;
} else {
return -1;
}
}
if (data[probe] == item) {
return probe;
}
if (data[probe] < item) {
lowEnd = probe + 1;
} else {
highEnd = probe - 1;
}
}
return -1;
}
5. Вывод
В этой статье мы рассмотрели интерполяционный поиск на примере. Мы также реализовали это на Java.
Примеры, показанные в этом руководстве, доступны на Github .