Найдите наименьший элемент K в двух отсортированных массивах в Java

1. Введение

В этой статье мы увидим, как найти k -й наименьший элемент в объединении двух отсортированных массивов.

Во-первых, мы определим точную проблему. Во-вторых, мы увидим два неэффективных, но простых решения. В-третьих, мы рассмотрим эффективное решение, основанное на бинарном поиске по двум массивам. Наконец, мы рассмотрим несколько тестов, чтобы убедиться, что наш алгоритм работает.

Мы также увидим фрагменты кода Java для всех частей алгоритма. Для простоты наша реализация будет работать только с целыми числами . Однако описанный алгоритм работает со всеми сопоставимыми типами данных и даже может быть реализован с помощью дженериков.

2. Что такое K -й наименьший элемент в объединении двух отсортированных массивов?

2.1. K - й наименьший элемент

Чтобы найти k -й наименьший элемент, также называемый статистикой k -го порядка, в массиве, мы обычно используем алгоритм выбора . Однако эти алгоритмы работают с одним несортированным массивом, тогда как в этой статье мы хотим найти k -й наименьший элемент в двух отсортированных массивах.

Прежде чем мы увидим несколько решений проблемы, давайте точно определим, чего мы хотим достичь. Для этого давайте сразу перейдем к примеру.

Нам даны два отсортированных массива ( a и b ), которые не обязательно должны иметь равное количество элементов:

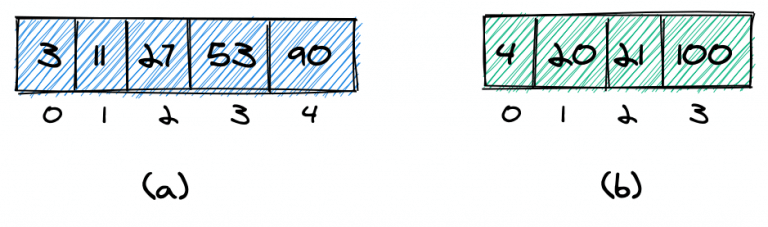
В этих двух массивах мы хотим найти k -й наименьший элемент. В частности, мы хотим найти k -й наименьший элемент в объединенном и отсортированном массиве:

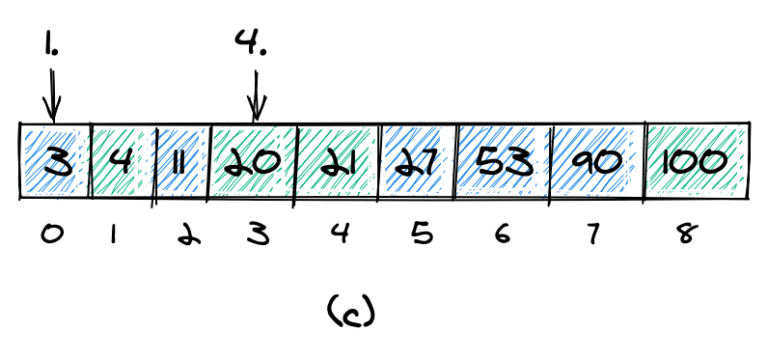
Объединенный и отсортированный массив для нашего примера показан на (c). 1- й наименьший элемент равен 3 , а 4- й наименьший элемент равен 20 .

2.2. Повторяющиеся значения

Нам также нужно определить, как обрабатывать повторяющиеся значения. Элемент может встречаться более одного раза в одном из массивов (элемент 3 в массиве a ), а также повторно встречаться во втором массиве ( b ).

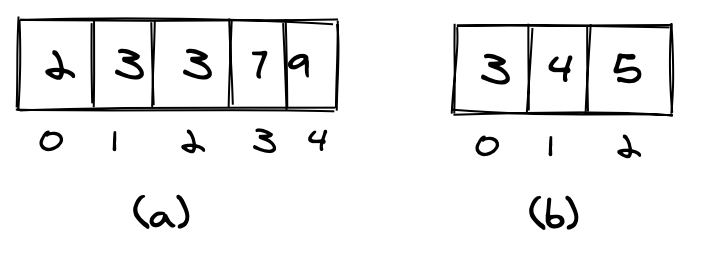
Если мы посчитаем дубликаты только один раз, мы будем считать, как показано в (c). Если мы посчитаем все вхождения элемента, мы будем считать, как показано в (d).

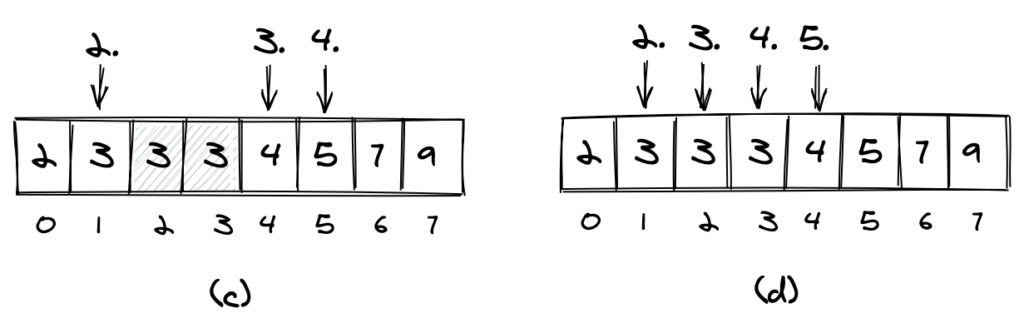
В оставшейся части этой статьи мы будем считать дубликаты, как показано в (d), таким образом, считая их, как если бы они были отдельными элементами.

3. Два простых, но менее эффективных подхода

3.1. Соедините, а затем отсортируйте два массива

Самый простой способ найти k -й наименьший элемент — соединить массивы, отсортировать их и вернуть k -й элемент результирующего массива:

int getKthElementSorted(int[] list1, int[] list2, int k) {

    int length1 = list1.length, length2 = list2.length;
    int[] combinedArray = new int[length1 + length2];
    System.arraycopy(list1, 0, combinedArray, 0, list1.length);
    System.arraycopy(list2, 0, combinedArray, list1.length, list2.length);
    Arrays.sort(combinedArray);

    return combinedArray[k-1];
}

Если n — длина первого массива, а m — длина второго массива, мы получаем общую длину c = n + m .

Поскольку сложность сортировки составляет O(c log c) , общая сложность этого подхода равна O(n log n) .

Недостатком этого подхода является то, что нам нужно создать копию массива, что требует больше места.

3.2. Объединить два массива

Подобно одному шагу алгоритма сортировки слиянием , мы можем объединить два массива, а затем напрямую получить k -й элемент.

Основная идея алгоритма слияния состоит в том, чтобы начать с двух указателей, которые указывают на первые элементы первого и второго массивов (a).

Затем мы сравниваем два элемента ( 3 и 4 ) по указателям, добавляем меньший элемент ( 3 ) к результату и перемещаем этот указатель на одну позицию вперед (b). Снова сравниваем элементы по указателям и добавляем к результату меньший ( 4 ).

Продолжаем таким же образом, пока все элементы не будут добавлены в полученный массив. Если один из входных массивов не имеет больше элементов, мы просто копируем все оставшиеся элементы другого входного массива в результирующий массив.

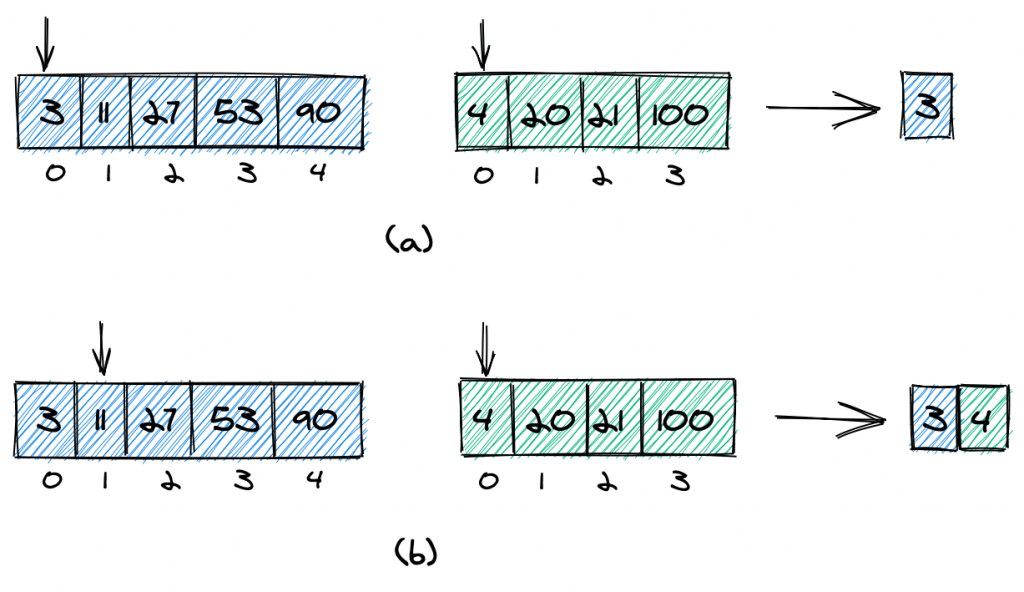
Мы можем улучшить производительность, если не будем копировать полные массивы, а остановимся, когда в результирующем массиве будет k элементов. Нам даже не нужно создавать дополнительный массив для объединенного массива, а можно работать только с исходными массивами.

Вот реализация на Java:

public static int getKthElementMerge(int[] list1, int[] list2, int k) {

    int i1 = 0, i2 = 0;

    while(i1 < list1.length && i2 < list2.length && (i1 + i2) < k) {
        if(list1[i1] < list2[i2]) {
            i1++;
        } else {
            i2++;
        }
    }

    if((i1 + i2) < k) {
        return i1 < list1.length ? list1[k - i2 - 1] : list2[k - i1 - 1]; 
    } else if(i1 > 0 && i2 > 0) {
        return Math.max(list1[i1-1], list2[i2-1]);
    } else {
        return i1 == 0 ? list2[i2-1] : list1[i1-1];
    }
}

Несложно понять, что временная сложность этого алгоритма составляет O( k ). Преимущество этого алгоритма в том, что его можно легко адаптировать для учета повторяющихся элементов только один раз .

4. Бинарный поиск по обоим массивам

Можем ли мы сделать лучше, чем O( k )? Ответ заключается в том, что мы можем. Основная идея состоит в том, чтобы выполнить алгоритм бинарного поиска по двум массивам .

Чтобы это работало, нам нужна структура данных, которая обеспечивает постоянный доступ для чтения ко всем ее элементам. В Java это может быть массив или ArrayList .

Давайте определим скелет метода, который мы собираемся реализовать:

int findKthElement(int k, int[] list1, int[] list2)
    throws NoSuchElementException, IllegalArgumentException {

    // check input (see below)

    // handle special cases (see below)

    // binary search (see below)
}

Здесь мы передаем k и два массива в качестве аргументов. Во-первых, мы проверим ввод; во-вторых, мы обрабатываем некоторые особые случаи, а затем выполняем бинарный поиск. В следующих трех разделах мы рассмотрим эти три шага в обратном порядке, поэтому сначала мы увидим бинарный поиск, затем — особые случаи и, наконец, проверку параметров.

4.1. Бинарный поиск

Стандартный бинарный поиск, когда мы ищем определенный элемент, имеет два возможных результата: либо мы находим искомый элемент, и поиск завершается успешно, либо мы его не находим, и поиск завершается неудачно. В нашем случае все по-другому, когда мы хотим найти k -й наименьший элемент. Здесь у нас всегда есть результат.

Давайте посмотрим, как это реализовать.

4.1.1. Поиск правильного количества элементов из обоих массивов

Мы начинаем наш поиск с определенного количества элементов из первого массива. Назовем этот номер nElementsList1 . Поскольку всего нам нужно k элементов, число nElementsList1 равно:

int nElementsList2 = k - nElementsList1;

Например, пусть k = 8 . Начнем с четырех элементов из первого массива и четырех элементов из второго массива (а).

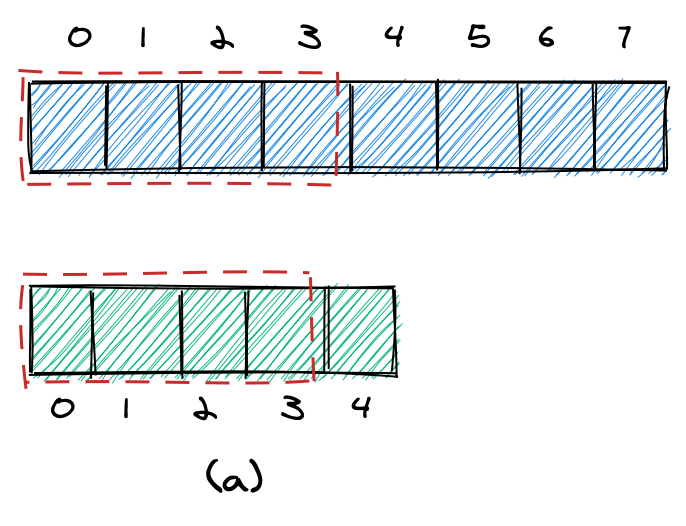
Если 4-й элемент в первом массиве больше, чем 4-й элемент во втором массиве, мы знаем, что мы взяли слишком много элементов из первого массива, и можем уменьшить nElementsList1 (b). В противном случае мы знаем, что взяли слишком мало элементов и можем увеличить nElementsList1 (b').

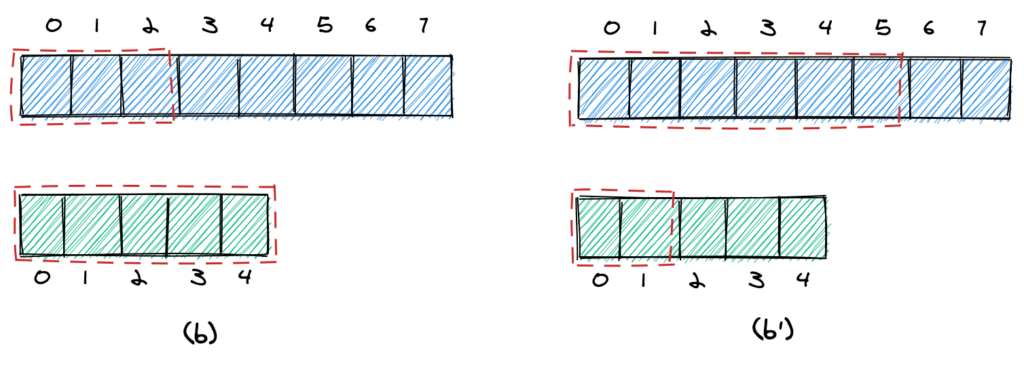
Мы продолжаем, пока не достигнем критерия остановки. Прежде чем мы посмотрим, что это такое, давайте посмотрим на код того, что мы описали до сих пор:

int right = k;
int left = = 0;
do {
    nElementsList1 = ((left + right) / 2) + 1;
    nElementsList2 = k - nElementsList1;

    if(nElementsList2 > 0) {
        if (list1[nElementsList1 - 1] > list2[nElementsList2 - 1]) {
            right = nElementsList1 - 2;
        } else {
            left = nElementsList1;
        }
    }
} while(!kthSmallesElementFound(list1, list2, nElementsList1, nElementsList2));

4.1.2. Критерии остановки

Мы можем остановиться в двух случаях. Во-первых, мы можем остановиться, если максимальный элемент, который мы берем из первого массива, равен максимальному элементу, который мы берем из второго (c). В этом случае мы можем просто вернуть этот элемент.

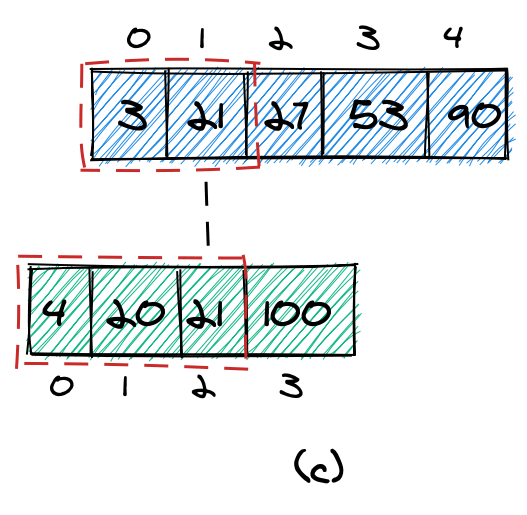
Во-вторых, мы можем остановиться, если выполняются следующие два условия (d):

• Самый большой элемент, который нужно взять из первого массива, меньше наименьшего элемента, который мы не берем из второго массива ( 11 < 100 ).
• Самый большой элемент, который нужно взять из второго массива, меньше, чем самый маленький элемент, который мы не берем из первого массива ( 21 < 27 ).

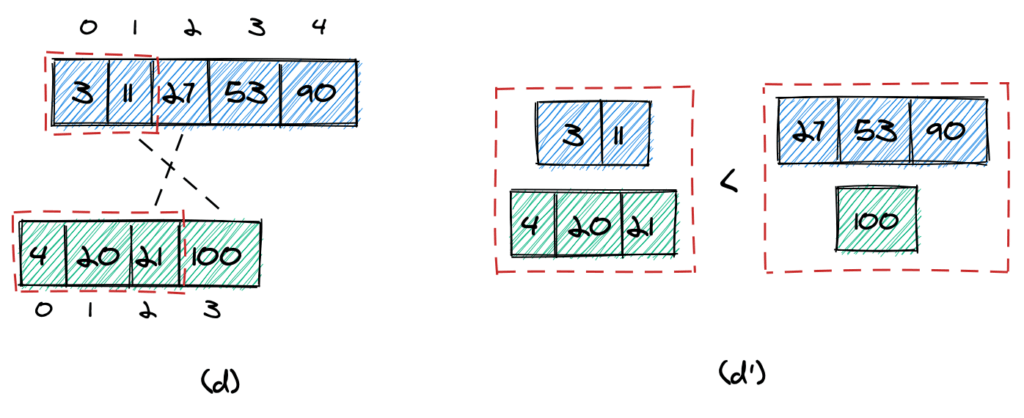
Легко представить (d'), почему это условие работает: все элементы, которые мы берем из двух массивов, наверняка меньше, чем любой другой элемент в этих двух массивах.

Вот код для критериев остановки:

private static boolean foundCorrectNumberOfElementsInBothLists(int[] list1, int[] list2, int nElementsList1, int nElementsList2) {

    // we do not take any element from the second list
    if(nElementsList2 < 1) {
        return true;
    }

    if(list1[nElementsList1-1] == list2[nElementsList2-1]) {
        return true;
    }

    if(nElementsList1 == list1.length) {
        return list1[nElementsList1-1] <= list2[nElementsList2];
    }

    if(nElementsList2 == list2.length) {
        return list2[nElementsList2-1] <= list1[nElementsList1];
    }

    return list1[nElementsList1-1] <= list2[nElementsList2] && list2[nElementsList2-1] <= list1[nElementsList1];
}

4.1.3. Возвращаемое значение

Наконец, нам нужно вернуть правильное значение. Здесь у нас есть три возможных случая:

• Мы не берем элементы из второго массива, поэтому целевое значение находится в первом массиве (e)
• Целевое значение находится в первом массиве (e')
• Целевое значение находится во втором массиве (e”)

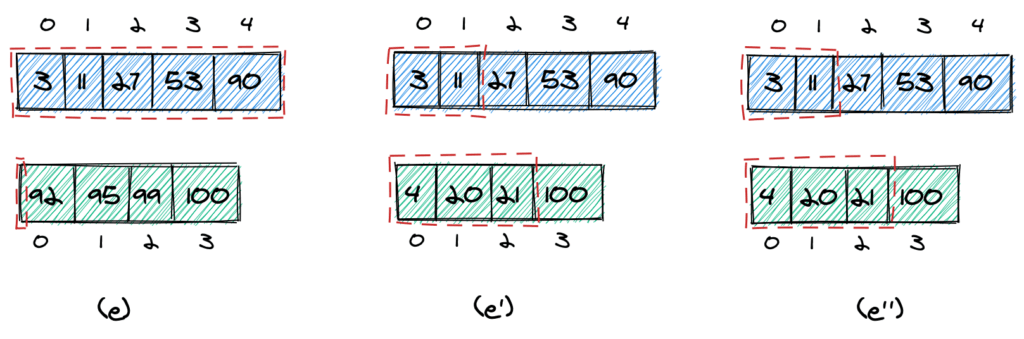
Давайте посмотрим на это в коде:

return nElementsList2 == 0 ? list1[nElementsList1-1] : max(list1[nElementsList1-1], list2[nElementsList2-1]);

Обратите внимание, что нам не нужно обрабатывать случай, когда мы не берем ни одного элемента из первого массива — мы исключим этот случай при обработке особых случаев позже.

4.2. Начальные значения для левой и правой границ

До сих пор мы инициализировали правую и левую границу для первого массива с помощью k и 0 :

int right = k;
int left = 0;

Однако в зависимости от значения k нам необходимо адаптировать эти границы.

Во- первых, если k превышает длину первого массива, нам нужно взять последний элемент в качестве правой границы. Причина этого довольно проста, так как мы не можем взять из массива больше элементов, чем есть.

Во- вторых, если k больше, чем количество элементов во втором массиве, мы точно знаем, что нам нужно взять как минимум (k – length(list2)) из первого массива. Например, пусть k = 7 . Поскольку второй массив имеет только четыре элемента, мы знаем, что нам нужно взять как минимум 3 элемента из первого массива, поэтому мы можем установить L равным 2:

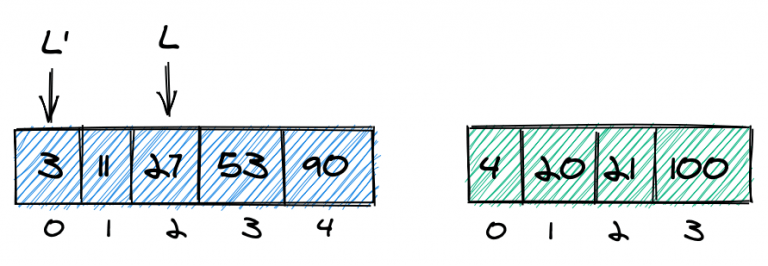
Вот код для адаптированных левой и правой границ:

// correct left boundary if k is bigger than the size of list2
int left = k < list2.length ? 0 : k - list2.length - 1;

// the inital right boundary cannot exceed the list1
int right = min(k-1, list1.length - 1);

4.3. Обработка особых случаев

Прежде чем приступить к собственно бинарному поиску, мы можем обработать несколько особых случаев, чтобы сделать алгоритм чуть менее сложным и избежать исключений. Вот код с пояснениями в комментариях:

// we are looking for the minimum value
if(k == 1) {
    return min(list1[0], list2[0]);
}

// we are looking for the maximum value
if(list1.length + list2.length == k) {
    return max(list1[list1.length-1], list2[list2.length-1]);
}

// swap lists if needed to make sure we take at least one element from list1
if(k <= list2.length && list2[k-1] < list1[0]) {
    int[] list1_ = list1;
    list1 = list2;
    list2 = list1_;
}

4.4. Проверка ввода

Давайте сначала посмотрим на проверку ввода. Чтобы предотвратить сбой алгоритма и выброс, например, NullPointerException или ArrayIndexOutOfBoundsException, мы хотим убедиться, что три параметра соответствуют следующим условиям:

• Оба массива не должны быть нулевыми и содержать хотя бы один элемент
• k должен быть >= 0 и не может быть больше, чем длина двух массивов вместе

Вот наша проверка в коде:

void checkInput(int k, int[] list1, int[] list2) throws NoSuchElementException, IllegalArgumentException {

    if(list1 == null || list2 == null || k < 1) { 
        throw new IllegalArgumentException(); 
    }
 
    if(list1.length == 0 || list2.length == 0) { 
        throw new IllegalArgumentException(); 
    } 

    if(k > list1.length + list2.length) {
        throw new NoSuchElementException();
    }
}

4.5. Полный код

Вот полный код алгоритма, который мы только что описали:

public static int findKthElement(int k, int[] list1, int[] list2) throws NoSuchElementException, IllegalArgumentException {

    checkInput(k, list1, list2);

    // we are looking for the minimum value
    if(k == 1) {
        return min(list1[0], list2[0]);
    }

    // we are looking for the maximum value
    if(list1.length + list2.length == k) {
        return max(list1[list1.length-1], list2[list2.length-1]);
    }

    // swap lists if needed to make sure we take at least one element from list1
    if(k <= list2.length && list2[k-1] < list1[0]) {
        int[] list1_ = list1;
        list1 = list2;
        list2 = list1_;
    }

    // correct left boundary if k is bigger than the size of list2
    int left = k < list2.length ? 0 : k - list2.length - 1; 

    // the inital right boundary cannot exceed the list1 
    int right = min(k-1, list1.length - 1); 

    int nElementsList1, nElementsList2; 

    // binary search 
    do { 
        nElementsList1 = ((left + right) / 2) + 1; 
        nElementsList2 = k - nElementsList1; 

        if(nElementsList2 > 0) {
            if (list1[nElementsList1 - 1] > list2[nElementsList2 - 1]) {
                right = nElementsList1 - 2;
            } else {
                left = nElementsList1;
            }
        }
    } while(!kthSmallesElementFound(list1, list2, nElementsList1, nElementsList2));

    return nElementsList2 == 0 ? list1[nElementsList1-1] : max(list1[nElementsList1-1], list2[nElementsList2-1]);
}

private static boolean foundCorrectNumberOfElementsInBothLists(int[] list1, int[] list2, int nElementsList1, int nElementsList2) {

    // we do not take any element from the second list
    if(nElementsList2 < 1) {
        return true;
    }

    if(list1[nElementsList1-1] == list2[nElementsList2-1]) {
        return true;
    }

    if(nElementsList1 == list1.length) {
        return list1[nElementsList1-1] <= list2[nElementsList2];
    }

    if(nElementsList2 == list2.length) {
        return list2[nElementsList2-1] <= list1[nElementsList1];
    }

    return list1[nElementsList1-1] <= list2[nElementsList2] && list2[nElementsList2-1] <= list1[nElementsList1];
}

5. Тестирование алгоритма

В нашем репозитории GitHub есть много тестовых случаев, которые охватывают множество возможных входных массивов, а также множество крайних случаев.

Здесь мы укажем только один из тестов, который проверяет не статические входные массивы, а сравнивает результат нашего алгоритма двойного бинарного поиска с результатом простого алгоритма соединения и сортировки. Вход состоит из двух рандомизированных массивов:

int[] sortedRandomIntArrayOfLength(int length) {
    int[] intArray = new Random().ints(length).toArray();
    Arrays.sort(intArray);
    return intArray;
}

Следующий метод выполняет один единственный тест:

private void random() {

    Random random = new Random();
    int length1 = (Math.abs(random.nextInt())) % 1000 + 1;
    int length2 = (Math.abs(random.nextInt())) % 1000 + 1;

    int[] list1 = sortedRandomIntArrayOfLength(length1);
    int[] list2 = sortedRandomIntArrayOfLength(length2);

    int k = (Math.abs(random.nextInt()) + 1) % (length1 + length2);

    int result = findKthElement(k, list1, list2);
    int result2 = getKthElementSorted(list1, list2, k);
    int result3 = getKthElementMerge(list1, list2, k);

    assertEquals(result2, result);
    assertEquals(result2, result3);
}

И мы можем вызвать вышеуказанный метод для запуска большого количества тестов:

@Test
void randomTests() {
    IntStream.range(1, 100000).forEach(i -> random());
}

6. Заключение

В этой статье мы увидели несколько способов найти k -й наименьший элемент в объединении двух отсортированных массивов. Сначала мы увидели простой и понятный алгоритм O(n log n) , затем версию со сложностью O(n) и, наконец, алгоритм, работающий за O(log n) .

Последний алгоритм, который мы видели, — хорошее теоретическое упражнение; однако для большинства практических целей нам следует рассмотреть возможность использования одного из первых двух алгоритмов, которые намного проще, чем бинарный поиск по двум массивам. Конечно, если производительность является проблемой, бинарный поиск может быть решением.

Весь код в этой статье доступен на GitHub.