12 записей с тегом "Структуры Данных"

1. Введение​

В этом руководстве мы рассмотрим реализацию двоичного дерева в Java.

Для этого руководства мы будем использовать отсортированное двоичное дерево , содержащее значения int .

2. Бинарное дерево​

1. Обзор​

В этой статье мы собираемся изучить алгоритм поиска по дереву Монте-Карло (MCTS) и его приложения.

Мы подробно рассмотрим его этапы, реализовав игру «Крестики-нолики» на Java . Мы разработаем общее решение, которое можно будет использовать во многих других практических приложениях с минимальными изменениями.

2. Введение​

Проще говоря, поиск по дереву Монте-Карло — это алгоритм вероятностного поиска. Это уникальный алгоритм принятия решений из-за его эффективности в открытых средах с огромным количеством возможностей.

1. Обзор​

В этом руководстве мы рассмотрим поиск в глубину в Java.

Поиск в глубину (DFS) — это алгоритм обхода, используемый как для структур данных Tree, так и для Graph . Поиск в глубину углубляется в каждую ветвь, прежде чем переходить к изучению другой ветви .

В следующих разделах мы сначала рассмотрим реализацию дерева, а затем графа.

Чтобы узнать, как реализовать эти структуры в Java, ознакомьтесь с нашими предыдущими руководствами по двоичному дереву и графику .

2. Поиск в глубину дерева​

1. Обзор​

Реверсирование бинарного дерева — одна из задач, которую нам могут предложить решить во время технического собеседования .

В этом кратком руководстве мы увидим несколько различных способов решения этой проблемы.

2. Бинарное дерево​

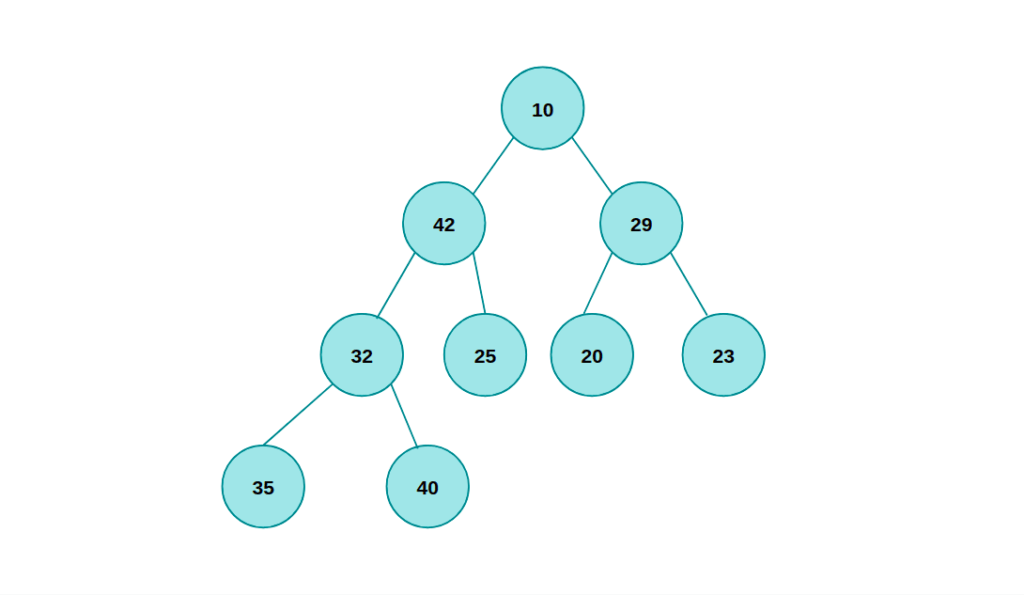
Двоичное дерево — это структура данных, в которой каждый элемент имеет не более двух дочерних элементов , называемых левым дочерним элементом и правым дочерним элементом. Верхний элемент дерева — это корневой узел, а дочерние — внутренние узлы .

1. Введение​

В этом руководстве мы обсудим различные варианты реализации структуры данных LIFO с поддержкой потоков .

В структуре данных LIFO элементы вставляются и извлекаются в соответствии с принципом «последним пришел – первым вышел». Это означает, что последний вставленный элемент извлекается первым.

В информатике стек — это термин, используемый для обозначения такой структуры данных.

Стек удобен для решения некоторых интересных задач , таких как оценка выражений, реализация операций отмены и т. д. Поскольку его можно использовать в средах параллельного выполнения, нам может потребоваться сделать его потокобезопасным.

2. Понимание стеков​

1. Обзор​

В этой быстрой статье мы познакомимся с классом java.util.Stack и начнем рассматривать, как мы можем его использовать.

Стек — это универсальная структура данных, которая представляет набор объектов в порядке LIFO (последним пришел — первым вышел), что позволяет помещать/извлекать элементы за постоянное время .

Для новых реализаций мы должны отдавать предпочтение интерфейсу Deque и его реализациям . Deque определяет более полный и непротиворечивый набор операций LIFO. Однако нам все еще может понадобиться иметь дело с классом Stack , особенно в устаревшем коде, поэтому важно хорошо его понимать.

2. Создайте стек​

1. Обзор​

В этом руководстве мы рассмотрим, как реализовать кучу min-max в Java.

2. Мин-макс куча​

Прежде всего, давайте посмотрим на определение и характеристики кучи. Минимальная куча — это полное бинарное дерево с признаками минимальной кучи и максимальной кучи:

1. Обзор​

Коллекции в Java основаны на паре основных интерфейсов и более чем дюжине классов реализации. Широкий выбор различных реализаций иногда может привести к путанице.

Принятие решения о том, какой тип коллекции использовать для конкретного варианта использования, — нетривиальная задача. Это решение может сильно повлиять на читаемость и производительность нашего кода.

Вместо того, чтобы объяснять все типы коллекций в одной статье, мы расскажем о трех наиболее распространенных: ArrayList, LinkedList и HashMap. В этом руководстве мы рассмотрим, как они хранят данные, их производительность и порекомендуем, когда их использовать.

2. Коллекции​

1. Введение​

В этом руководстве мы рассмотрим реализацию кругового связанного списка в Java.

2. Круговой связанный список​

Циклический связанный список — это вариант связанного списка , в котором последний узел указывает на первый узел, завершая полный круг узлов . Другими словами, этот вариант связанного списка не имеет пустого элемента в конце.

Благодаря этому простому изменению мы получаем некоторые преимущества:

1. Обзор​

Структуры данных представляют собой важнейший актив в компьютерном программировании, и очень важно знать, когда и зачем их использовать.

Эта статья представляет собой краткое введение в структуру данных trie (произносится как «попробуй»), ее реализацию и анализ сложности.

2. Попробуйте​

Trie — это дискретная структура данных, которая не очень хорошо известна или широко упоминается в типичных курсах по алгоритмам, но, тем не менее, важна.